The tidiness of elementary mathematics: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(→‎Applets)
(→‎Applets)
Zeile 15: Zeile 15:
  
  
−
 
+
<ggb_applet width="634" height="463"  version="4.0" ggbBase64="UEsDBBQACAAIAJx0aD8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAJx0aD8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVjrbts2FP7dPsWBUAwJmtiibrY7u8VaoFiBtCuQbii2rgAl0TYbmVRFypde/u199k57kh2SkiynaZauw2ok4e3wXL5z4YmnD7arAtasUlyKmUcGvgdMZDLnYjHzaj0/HXsP7t+eLphcsLSiMJfViuqZFxlKnuMkz/NxnmanGQ2T0ygYZ6eThJHTbD4nScYiGqfEA9gqfk/IZ3TFVEkzdp4t2YqeyYxqK3ipdXlvONxsNoNW1EBWi+FikQ62KvcA1RRq5jWTe8ju4NImtOSB75Phy6dnjv0pF0pTkTEPjAk1v3/71nTDRS43sOG5Xs68JEYzlowvlmhT4uNiaIhKBKRkmeZrpvBqb2lt1qvSs2RUmPNbbgZFZ44HOV/znFUzzx+E/iiZBN3fkQey4kzohpY0Moctt+mas41ja2YOZQ+0lEVKDUf48AECP/DhxAzEDQEOSeKOfLfnh24I3BC5IXY0kbseOdLI0USOJgo9WHPF04LNvDktFCLIxbxC73VrpXcFs/o0G3vryQnapPg7JA4NpA5y3Pf9E/OLOJ9ELdY9I0lPqq7qLxTaikzC6OYig68yNGxlBleZGcSfMTO5Rqiz+yZ2krgnE0XZH/v7icTwOjMvS3TrrxOYRP+LidNhmyrTJjtALQ1tEz2arZTJl3AC8cSEPYEYcyMZYZTHQCY4jALAbAASQxTjkowhMeMIwhEeRBDCGAwdCcEmRzzGP9HIMksgRmZmd4Q5CQQFRRCHQGxORYCZBDYvMUeDECniGGK8ZMSTwLAIE4gSXIVjiFBHk5IjgoQhXsQ1ig8gJBCay2QEQQKJ4Ucik+rJ2KiOLANIfEiIYYhZjRntshnpxxAaa5IGLi7KWh9AlK3ydqpl2fkCqbEe7aueq08HRfHWtKApK/CdODeeBFjTwmSEFTSXQkPrxMDtLSpaLnmmzpnWeEvBG7qmZ1Sz7WOkVq1sS5tJoZ5XUj+SRb0SCiCThd/pLAvSmwed1rgIewdR/yDuHSS9+ehKuRJPoFYM5ctKteQ0z58Yin1pQCR/EsXuYcXoRSn5oRnToX1ypqzOCp5zKn7BYDVSDC7QvUCmXLUvUBTGrSKyys93CiMYtr+ySiK0sX1zd24VTCZmpTJqUiwMB2H/Q5Dn7nNnTgJbd46gW9bZuKhM/jb2mcUT9VAW+y1r5SNa6rqyLQKWwMro/oNYFMxGgs1ffH+zi1Ruz10IhI7Xi12JK98pkC4suoAVIIhjJGjG1I2WxmjWUfmWxrcUfhtTPO/OySSwFHZM3WipMEidao2lpDWT+K0Yrmzd8r2D7LARbl7zWnB91i40zy72lhr6Z/UqZV2cHLIk/xHL6fBSHE0vWCVY0YQterKWtXJZ2IvonGV8hUt30ABCjbN+RgXcbs4WFWv1Lmzz5eCyp34/Ij/ZtqweV3L1RKxfYCRcUmA6bLWcqqzipQk4SLHUX7B9TOVcUXwp8v49k2doemZeBIRHG2gwA2u9lJXtr7Bw4GjSq2Ar7KZA2+AS9YpVPOuAFrZRQ6XqRu940GhuUAaZvsGKdsk5ey/i8WfCD2hRLqlp75p8KuiOVQfQWG5PZd4IbuhUYfpCWHF86LC5hhXd2kAEmiqsdhpbY3SG2LfGTrWmWmCjYdIerwSRne2waNhKMOfbHqSIEn+HUUEPzNkngsZKfIHtprItkG7y0k5+5HnORKcvFRg/1gtYjEoXnyVjLrK7iyWab+tBz/ONY4yLtmWFsgyTBuI5/puxNe/N0fYYZnBE4C5sYQji+PWROHYP0KFj57WwweDtWVzvxV4S3MSN/g3d6P9bKK8DBGbeokFk4RD5648/X+PMuwEQi28KxOX4MAlxswj5JxDJl6KIdrOtJg2Q372tpf7+Drwq2FwfAZC7r7ABzd5vP74XH+GVfbWOXwvE+ioSdxuj8uiMvmAvfxO/H+PC7e5vX0cFd9x4VTAbPb1Dpb+lD7my6ru9fbmwXZzCcjrvmnb7nPtN997dx/+yK/3cdAZgSpM/iMd+/0NsncLKi23JO/ctwyVXDvv13rZOzbcA9/8GUEsHCPcAZm4ABgAAohAAAFBLAQIUABQACAAIAJx0aD/WN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAnHRoP/cAZm4ABgAAohAAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACXBgAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
−
<ggb_applet width="634" height="463"  version="4.0" ggbBase64="UEsDBBQACAAIAEl0aD8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAEl0aD8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVfrbts2FP7dPsWBUAwJmsSibnY6u8VaoFiBtCuQbiiGogAl0TIbmVRFylZ6+bf32TvtSXZISrKctlm6DquRmLfDc/nOhcfzB+26hA2rFZdi4ZET3wMmMplzUSy8Ri+PZ96D+7fnBZMFS2sKS1mvqV54kaHkOU7yPJ/laXac0TA5joJZdnyaMHKcLZckyVhE45R4AK3i94R8RtdMVTRj59mKremZzKi2gldaV/cmk+12e9KLOpF1MSmK9KRVuQeoplALr5vcQ3Z7l7ahJQ98n0xePj1z7I+5UJqKjHlgTGj4/du35lsucrmFLc/1auElMZqxYrxYoU2Jj4uJIaoQkIplmm+YwqujpbVZryvPklFhzm+5GZSDOR7kfMNzVi88/yT0p8lpMHxPPZA1Z0J3tKSTOem5zTecbR1bM3Moe6ClLFNqOMKHDxD4gQ9HZiBuCHBIEnfkuz0/dEPghsgNsaOJ3PXIkUaOJnI0UejBhiuelmzhLWmpEEEuljV6b1grfVkyq0+3sbOeHKFNir9D4tBA6iDHfd8/Mv+I81HUYz0ykoyk6rr5SqG9yCSMbi4y+CZDw15m8Dkzg/gLZibXCHV238ROEo9koij7Z/8/kRheZ+ZViW79bQKT6H8xcT7pU2XeZQeolaHtokeztTL5Ep5CfGrCnkCMuZFMMcpjIKc4TAPAbAASQxTjkswgMeMUwikeRBDCDAwdCcEmRzzDr2hqmSUQIzOzO8WcBIKCIohDIDanIsBMApuXmKNBiBRxDDFeMuJJYFiECUQJrsIZRKijSckpQcIQL+IaxQcQEgjNZTKFIIHE8CORSfVkZlRHlgEkPiTEMMSsxox22Yz0MwiNNUkHFxdVo/cgytZ5P9WyGnyB1FiPdlXP1ae9onhrXtKUlfhOnBtPAmxoaTLCClpKoaF3YuD2ippWK56pc6Y13lLwhm7oGdWsfYzUqpdtaTMp1PNa6keybNZCAWSy9AedZUlG82DQGhfh6CAaH8Sjg2Q0n35WrsQTaBRD+bJWPTnN8yeGYlcaEMlfRHn5sGb0opJ834z5xD45c9ZkJc85Fb9hsBopBhcYXiBTrvoXKArjXhFZ5+eXCiMY2t9ZLbHGkNi8uZduFZrV+IM+Vhk1+Rb7lm60Gn+IE8A2gx9oywYTi9qkb2eeWTxRD2W527JGPqKVbmrbIWAFrI3qP4miZDYQbPri85tdpLI9dxEQOl4vLitc+U6BtLDgAhaAII6RoBtTN1oao9lA5Vsa31L4fUjxfDgnp4GlsGPqRkuFMepU6ywlvZnE78VwZcuW7+0lhw1w85g3guuzfqF5drGz1NA/a9YpG8JknyX5j1jOJ1fCaH7BasHKLmrRk41slEvCUUDnLONrXLqDDhBqnPUrKuB2c1bUrNe7tL2Xg8ue+uOA/GTbsnpcy/UTsXmBkXBFgfmk13KusppXJuAgxUp/wXYxlXNF8aHIx/dMmqHpmXkQEB5toMEEbPRK1ra9wrqBo8mukq2xmQJtg0s0a1bzbABa2D4NlWo6vU2HazU3KINM32BBu+KcnRfx+AvhB7SsVtR0d10+lfSS1XvQWG5PZd4L7sSWpi2ENcd3DntrWNPWBiLQVGGx09gZozPErjN2qnXFAvsMk9t4JYhclmPNODWTJW9HkCJK/B1GBd0zZ5cIGgvxBXabynZAustLO/mZ5zkTg75UYPxYL2Atqlx8Voy5yB4uVmi+rQcjz3eOMS5qqxplGSYdxEv8ldGa5+agPYQFHBC4Cy1MQBy+PhCH7v3Zd+yyETYYvB2L6704SoKbuNG/oRv9fwvldYDAwis6RAqHyF9//PkaZ94NgCi+KxBX48MkxM0i5J9AJF+LItrNWk06IH9420j94x14VbKlPgAgd19h/5m9bz++Fx/hlX21Dl8LuOMIP4O04ebts/6eSHN1Rl+wl25vl9S21VJY9JZDZ20fXb9rsYf7+FO41s/N+w2mgPgn8exKY2CqCXYV2I+8GwrlGPDJuCrb/qb7qX7/b1BLBwiIiICg5gUAAEcQAABQSwECFAAUAAgACABJdGg/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAEl0aD+IiICg5gUAAEcQAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAfQYAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
+

Version vom 8. November 2011, 23:37 Uhr

We all expect a certain tidiness to mathematics, and for many this provides a gratifying aesthetic pleasure. However, there are some wrinkles. One of these arises in the integral of 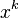x^k. Calculus provides us with the formula 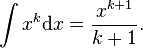\int x^k\mathrm{d}x = \frac{x^{k+1}}{k+1}. However, this equation is only correct for 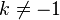k\neq -1. If we try to take 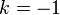k=-1 the right hand side is meaningless because we have a zero on the denominator of the fraction, i.e. \frac{1}{0}. 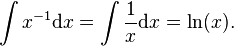But in this case a separate argument gives the answer \int x^{-1}\mathrm{d}x = \int \frac{1}{x}\mathrm{d}x = \ln(x).

Our expectation is that these two formulae should be reconciled. Indeed, if we let 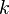k approach 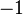-1 in the first we should end up with the second, but that fails to happen. For each 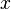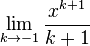x, \lim_{k\rightarrow -1} \frac{x^{k+1}}{k+1} is undefined.

This vingette explores this issue.

Main article

Applets


Von „http://dmuw.zum.de/index.php?title=The_tidiness_of_elementary_mathematics&oldid=30224“