Higher Dimensions: Unterschied zwischen den Versionen
K (→Projections) |
K (→Projections) |
||
| Zeile 146: | Zeile 146: | ||
<br/> | <br/> | ||
<math>g_{i}: \ \vec{X}= \vec{A_{i}} + k \cdot \begin{pmatrix}1 \\ \vdots \\1 \end{pmatrix} , \ \ (1\le i \le 2^{n})</math> and the ''(n-1)''-hyper-plane <math>R:\ x_{1}+ \cdots +x_{2}=0.</math> | <math>g_{i}: \ \vec{X}= \vec{A_{i}} + k \cdot \begin{pmatrix}1 \\ \vdots \\1 \end{pmatrix} , \ \ (1\le i \le 2^{n})</math> and the ''(n-1)''-hyper-plane <math>R:\ x_{1}+ \cdots +x_{2}=0.</math> | ||
| + | <br/> | ||
| + | <br/> | ||
| + | The vector (1,1,...,1) is orthogonal to the plane ''R'', the line g<sub>i</sub> is the orthogonal line to the plane through the vertices. After considering similarities of the projections above, such as vertices having the same image under these special mappings, we get the following representation for the corresponding orthogonal projection of a four-dimensional hyper cube into the three-dimensional space: | ||
| + | <br/> | ||
| + | <!--Bild Einfügen (Klein_Bild_4;Klein_Bild_5;SchülerBild?)--> | ||
| + | <br/> | ||
| + | Another possibility to describe orthogonal projections from ''n''-dimensional into ''k''-dimensional space <math>(k \le n)</math> uses the linearity of orthogonal projections (as linear transformations). This property can be used to create and understand two-dimensional images of cubes of any dimension. | ||
| + | <br/> | ||
| + | '''Example 4: Projection of a cube''' | ||
| + | Fig. 2 shows three generating vectors of the cube and their images under orthogonal projection along the body-diagonal. All vertices of the cube are linear combinations of these vectors with coefficients 0 and 1. The linearity of the projection leads to the same property for the images of all vertices. | ||
| + | <br/> | ||
| + | While describing the ''n''-dimensional cube with adequate linear combinations of n linear independent generating vectors, the following can be shown: For the ''n''-dimensional cube, there is an orthogonal projection into R<sup>2</sup> and an appropriate plane of projection, such that the images of the generating vectors point to the vertices of a regular ''n''-sided polygon. According to additivity, the images of all the other vertices finally result in corresponding linear combinations. (For ''n''=3 see Fig. 2 and Example 3, with the regular triangle as image of the generating vectors) | ||
| + | <br/> | ||
| + | To understand how the projection of an ''n''-dimensional hypercube on a ''k''-dimensional subspace is obtained we first explain how a cube is projected onto a line in the three-dimensional space: | ||
| + | <br/> | ||
| + | For each vertex of the cube take the plane orthogonal to the given line which contains this vertex. The intersection point of the plane and the line is the orthogonal projection of the vertex onto the line. | ||
| + | <br/> | ||
== Intersections of cubes == | == Intersections of cubes == | ||
Version vom 23. November 2011, 18:42 Uhr
Inhaltsverzeichnis |
Under Construction
This site is still under construction. For the full article please check the pdf version.
Looking for the next dimension
Does our world really have more than three dimensions? If so, do objects in higher dimension have a relation to the world around us? Is it possible to get a perception of these objects or do they withdraw any representation? Questions like these will be posed by students if you talk about space dimensions in school. Students want to understand the meaning of a four-, five or even n-dimensional space. The relativity theory uses four dimensions to explain the concept of space-time, six dimensions are necessary to describe the bending of space-time and different string theories even use representations in up to 26 dimensions (e.g. L. Botelho, R. Botelho, 1999). Another current domain of application for higher dimensional objects and their three-dimensional representations is the study of non-periodic structures in modern crystallography. Within the concept of quasicrystals projections of higher dimensional point-sets (such as the integer-lattice in dimension 5) to three dimensional space are supposed to be good models for non-periodic crystalline structures (see section 5 below).
These examples show one of the main characteristics of mathematical thinking: If it is easier or helpful to describe real phenomena in higher dimensional space, the three special dimensions can be extended. This can easily be explained under formal aspects. Thus, linear equations with three variables may be interpreted as a plane in space, linear equations with four variables are interpreted as a three dimensional hyper plane in a four dimensional space. Also, linear equations with n-variables are interpreted as an (n-1)-dimensional hyper plane in an n-dimensional space. While using more than three variables, the advantage of such an expansion of the dimension-concept benefits from a simpler and more consistent description of mathematical relations. It is not necessary for formal calculations on an algebraic and numerical level to have illustrative perceptions in such a higher dimensional context. Nevertheless, on the one hand this leads to the question how to translate the results of such considerations into the real world. On the other hand there is a need to describe at least basic objects of higher dimensions in our three dimensional space.
In the following, thoughts dealing with the development of representations of higher dimensional objects will be discussed by exemplarily considering a four-dimensional object, the four-dimensional cube. It will be shown that the approach to four- and higher-dimensional cubes can be done in different ways. The extensive use of analogical considerations serves as a basis for understanding higher dimensional objects. In the following, three different approaches will be shown and analyzed1.
(1) A systematic extension of the concept of coordinates,
(2) Projections of higher-dimensional objects on (hyper)planes,
(3) Intersections of (hyper)cubes and a (hyper)plane.
1 A detailed description of these approaches is found in Ruppert (2010)
Geometry of coordinates
The unit line segment and the unit square can be considered as a one‐ or two‐dimensional analog of the unit cube. Looking at the coordinates of the vertices in a coordinate system, we get
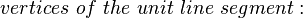
|
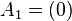
|
|
||
|
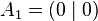
|
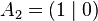
|
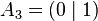
|
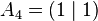
|
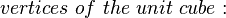
|
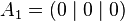
|
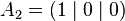
|
|
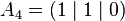
|
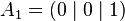
|
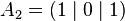
|
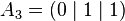
|
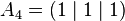
| |
By successively adding additional coordinates with coefficients 0 and 1, the coordinates of the vertices
and thus the number of vertices of a unit hyper cube in a four‐ or five‐dimensional coordinate system
are obtained. The transition to hyper cubes in higher dimensions can exclusively be accomplished on a
symbolical level and can be considered as a continuation of the concept of the coordinates.
Combinatorial considerations lead to the following relation for the number N(n;k) of the k‐dimensional
“boundary cubes” of an n‐dimensional cube (see e. g. Graumann, 2009):
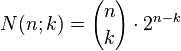
This formula can be obtained by the following observations:
- Every k‐dimensional “boundary‐cube” is parallel to a k‐dimensional hyperplane which is spanned by k generating vectors of the n‐dimensional cube (see also sec. 3). As a consequence, the coordinates of vertices belonging to one and the same k‐dimensional “boundary‐cube” differ in at most k coefficients (and all such vertices belong to this cube).
- There are
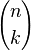 possibilities to choose k coefficients out of n.
possibilities to choose k coefficients out of n.
- There are 2n possibilities to choose a "starting vertex".
- There are 2k starting vertices leading to the same boundary cube.
Example 1: The three‐dimensional cube (n = 3):
| Number of vertices (k= 0): | 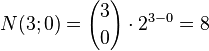
|
| Number of edges (k= 1): | 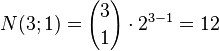
|
| Number of faces (k= 2): | 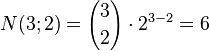
|
| Number of cubes (k= 3): | 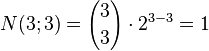
|
This can be illustrated in the following table:
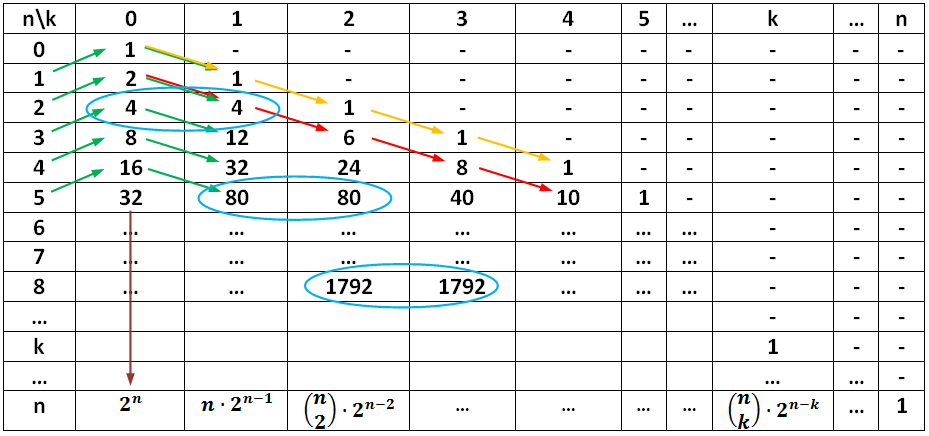
Table 1: Number of the k‐dimensional boundaries of an n‐dimensional cube
First of all, following the yellow highlights, the table allows the interpretation of a single point as a cube
of dimension 0, so that the formula above is consistent even for n = 0. The number sequences
highlighted in different colors lead to further conjectures, which can be proved by using the formula for
N(n;k) above. For instance:
-
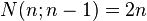 (red color)
(red color)
-
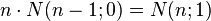 (green color)
(green color)
-
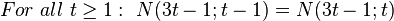 (blue color)
(blue color)
Moreover, a recursive formula is given, to calculate the data of the n‐dimensional cube of the corresponding numbers for the (n-1)‐dimensional cube
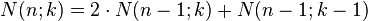 .
.
Example 2: Proof of the recursive formula
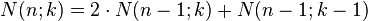
|

|
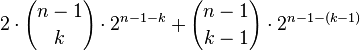
|

|
![\left[{n-1 \choose k}+{n-1 \choose k-1} \right] \cdot 2^{(n-k)}](/images/math/b/0/7/b07749b421b556ab0fce83f2278ee748.png)
| |

|
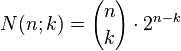
| |

|
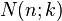
|
Of course, these algebraic arguments can easily be reinterpreted geometrically and retransformed to the geometric situation.
Projections
In the following, the basic idea of describing higher dimensional objects by means of projection will be generalized in higher dimensions. Especially the orthogonal projection along a body diagonal of an n-dimensional hyper cube (i.e. the line segment from (0, . . . , 0) to (1, . . ., 1)) in an (n-1)-dimensional space can easily be generalized.
Example 3: Projections of square and cube
For 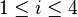 let Ai (Sec. 2) be the vertices of the square. The projection of Fig. 1 is represented by the intersection of the straight lines
let Ai (Sec. 2) be the vertices of the square. The projection of Fig. 1 is represented by the intersection of the straight lines
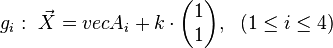 with the line
with the line 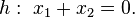
This is an orthogonal projection. Similarly, the orthogonal projection of an n-dimensional hyper cube is fully described by the projection of the coordinates of the vertices 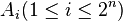 . We look for the intersection points of the straight lines:
. We look for the intersection points of the straight lines:
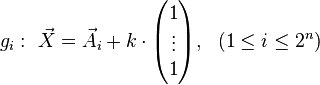 and the (n-1)-hyper-plane
and the (n-1)-hyper-plane 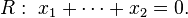
The vector (1,1,...,1) is orthogonal to the plane R, the line gi is the orthogonal line to the plane through the vertices. After considering similarities of the projections above, such as vertices having the same image under these special mappings, we get the following representation for the corresponding orthogonal projection of a four-dimensional hyper cube into the three-dimensional space:
Another possibility to describe orthogonal projections from n-dimensional into k-dimensional space 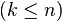 uses the linearity of orthogonal projections (as linear transformations). This property can be used to create and understand two-dimensional images of cubes of any dimension.
uses the linearity of orthogonal projections (as linear transformations). This property can be used to create and understand two-dimensional images of cubes of any dimension.
Example 4: Projection of a cube
Fig. 2 shows three generating vectors of the cube and their images under orthogonal projection along the body-diagonal. All vertices of the cube are linear combinations of these vectors with coefficients 0 and 1. The linearity of the projection leads to the same property for the images of all vertices.
While describing the n-dimensional cube with adequate linear combinations of n linear independent generating vectors, the following can be shown: For the n-dimensional cube, there is an orthogonal projection into R2 and an appropriate plane of projection, such that the images of the generating vectors point to the vertices of a regular n-sided polygon. According to additivity, the images of all the other vertices finally result in corresponding linear combinations. (For n=3 see Fig. 2 and Example 3, with the regular triangle as image of the generating vectors)
To understand how the projection of an n-dimensional hypercube on a k-dimensional subspace is obtained we first explain how a cube is projected onto a line in the three-dimensional space:
For each vertex of the cube take the plane orthogonal to the given line which contains this vertex. The intersection point of the plane and the line is the orthogonal projection of the vertex onto the line.

