Abschwächung der Gruppendefinition: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Die Seite wurde neu angelegt: „<math> </math> ==Aussage== Sei <math>(G,\cdot)</math> eine Halbgruppe (d.h. Zweistellige Verknüpfung + Abgeschlossenheit + Assoziativität). Hat G linksinver…“) |
Version vom 25. November 2018, 12:05 Uhr
Aussage
Sei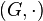 
eine Halbgruppe (d.h. Zweistellige Verknüpfung + Abgeschlossenheit + Assoziativität). Hat G linksinverse Elemente 
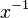und ein linksneutrales Element 
. Dann sind die linksinversen Elemente auch rechtsinvers und das linksneutrale Element auch rechtsneutral.
Beweis
Die Aussage enthält zwei Teilaussagen, die wir nacheinander beweisen:
1. Die linksinversen Elemente sind auch rechtsinvers.
- In mathematischer Schreibweise:
- Sei
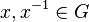und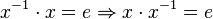 
2. Das linksneutrale Element ist auch rechtsneutral.
