Kürzbarkeit/Sudokuregel in Gruppen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 21: | Zeile 21: | ||
*Betrachten wir die Verknüpfungstabelle einer Gruppe. In diesem Fall eine endliche Gruppe mit 4 Elementen. Dann sehen wir, dass in jeder Spalte und jeder Zeile jedes Gruppenelement genau einmal vorkommt, wie bei einem Sudoku. | *Betrachten wir die Verknüpfungstabelle einer Gruppe. In diesem Fall eine endliche Gruppe mit 4 Elementen. Dann sehen wir, dass in jeder Spalte und jeder Zeile jedes Gruppenelement genau einmal vorkommt, wie bei einem Sudoku. | ||
| − | :Sei <math> a \text{ und } c \in G </math> fest gewählt. Wir überlegen, gibt es ein <math> b \in G </math> mit <math> \ast(a,b) = c </math> oder mit der '''Infixschreibweise''': <math> a \ast b = c </math> | + | :Sei <math> a \text{ und } c \in G </math> fest gewählt. Wir überlegen, gibt es ein <math> b \in G </math> mit <math> \ast(a,b) = c </math> oder mit der '''Infixschreibweise''': <math> a \ast b = c </math>. Das Element <math> a^{-1} \ast c </math> ist ein Element in G. Und es gilt: <math> \ast(a,a^{-1} \ast c) = c <\math>, oder in der Infixschreibweise: <math> a \ast a^{-1} \ast c = e \ast c = c </math>. Betrachten wir die Verknüpfungstafel, dann gilt: In der Reihe von a finde ich jedes beliebig andere Gruppenelement. |
| + | Gleichzeitig gilt wegen der Rechtskürzbarkeit, dass jedes Gruppenelement in jeder Reihe nur einmal vorkommt. | ||
[[Datei:Sudokuregel_2.jpg|center|800px]] | [[Datei:Sudokuregel_2.jpg|center|800px]] | ||
Version vom 4. Dezember 2018, 23:46 Uhr
Aussage
Alle Elemente einer Gruppe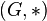 
sind links- und rechtskürzbar.
Erklärungen
Ein Element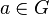 
heißt linkskürzbar, wenn für alle 
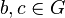gilt:
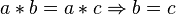
Entsprechend ist rechtskürzbar definiert.
Beweis
Aspekte
- Betrachten wir die Verknüpfungstabelle einer Gruppe. In diesem Fall eine endliche Gruppe mit 4 Elementen. Dann sehen wir, dass in jeder Spalte und jeder Zeile jedes Gruppenelement genau einmal vorkommt, wie bei einem Sudoku.
- Sei
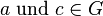fest gewählt. Wir überlegen, gibt es ein 
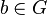mit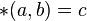 
oder mit der Infixschreibweise: 
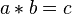. Das Element 
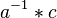ist ein Element in G. Und es gilt: Fehler beim Parsen(Unbekannte Funktion „\math“): \ast(a,a^{-1} \ast c) = c <\math>, oder in der Infixschreibweise: <math> a \ast a^{-1} \ast c = e \ast c = c
. Betrachten wir die Verknüpfungstafel, dann gilt: In der Reihe von a finde ich jedes beliebig andere Gruppenelement. Gleichzeitig gilt wegen der Rechtskürzbarkeit, dass jedes Gruppenelement in jeder Reihe nur einmal vorkommt.
