Übungsaufgaben zur Flächenberechnung am Dreieck: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(Unterseite)
 
(Bilder eingefügt)
Zeile 1: Zeile 1:
 
__NOTOC__
 
__NOTOC__
 
===Aufgabe 1===
 
===Aufgabe 1===
−
Berechne den Flächeninhalt der Dreiecke TIM, EVA und RON
+
Berechne den Flächeninhalt der Dreiecke TIM und EVA
  
−
===Aufgabe 2: Nussecke backen===
+
===Aufgabe 2: Wovon hängt der Flächeninhalt ab?===
 +
Bestimme, wovon der Flächeninhalt des darsgestellten Dreiecks abhängt.
 +
 
 +
[[Bild:Ebert_DreieckFrage.jpg|center]]
 +
 
 +
<quiz display="simple">
 +
{ Kreuze die richtige Antwort an }
 +
+c
 +
-<math>\alpha</math>
 +
+W
 +
-<math>\gamma</math>
 +
+Länge [AB]
 +
-<math>\beta</math>
 +
</quiz>
 +
 
 +
===Aufgabe 3: Nussecke backen===
 
[[Bild:Ebert_Nussecke.jpg|center]]
 
[[Bild:Ebert_Nussecke.jpg|center]]
 
:'''Maja hat 30 Nussecken gebacken und möchte deren Oberseite vollständig mit Schokolade überziehen. Das Bild zeigt eine Nussecke, die 6,7 cm hoch und 14,5 cm breit ist. Alle Nussecken sind gleich groß. <br>
 
:'''Maja hat 30 Nussecken gebacken und möchte deren Oberseite vollständig mit Schokolade überziehen. Das Bild zeigt eine Nussecke, die 6,7 cm hoch und 14,5 cm breit ist. Alle Nussecken sind gleich groß. <br>
Zeile 13: Zeile 28:
 
</div>
 
</div>
  
−
=== Aufgabe 3: Variation Dreieck===
+
=== Aufgabe 4: Variation Dreieck===
 
: '''Wie sieht die Flächeninhaltsformel für ein... <br>
 
: '''Wie sieht die Flächeninhaltsformel für ein... <br>
 
* ...rechtwinkliges Dreieck ABC aus?<br>'''
 
* ...rechtwinkliges Dreieck ABC aus?<br>'''
 
:Der rechte Winkel befindet sich am Eckpunkt C
 
:Der rechte Winkel befindet sich am Eckpunkt C
−
[[Bild:Ebert_rechtwinkligesDreieck.jpg|center]]
+
[[Bild:Ebert_rechtwinklig.jpg|center]]
 +
 
 
<quiz display="simple">
 
<quiz display="simple">
 
{Zu welchem speziellen Parallelogramm kann man das Dreieck ganz einfach ergänzen?}
 
{Zu welchem speziellen Parallelogramm kann man das Dreieck ganz einfach ergänzen?}
Zeile 39: Zeile 55:
 
:'''Wie sieht die Flächeninhaltsformel für ein...'''
 
:'''Wie sieht die Flächeninhaltsformel für ein...'''
 
* '''..gleichschenklig-rechtwinkliges Dreieck ABC aus?'''
 
* '''..gleichschenklig-rechtwinkliges Dreieck ABC aus?'''
−
:Der rechte Winkel befindet sich am Eckpunkt C. [[Bild:Ebert_gleichschenkligrwDreieck.jpg|center]]
+
:Der rechte Winkel befindet sich am Eckpunkt C.  
−
 
+
[[Bild:Ebert_gleichschenklig.jpg|center]]
 
<quiz display="simple">
 
<quiz display="simple">
  

Version vom 15. Juli 2009, 16:02 Uhr

Aufgabe 1

Berechne den Flächeninhalt der Dreiecke TIM und EVA

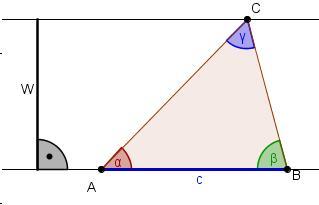
Aufgabe 2: Wovon hängt der Flächeninhalt ab?

Bestimme, wovon der Flächeninhalt des darsgestellten Dreiecks abhängt.

Ebert DreieckFrage.jpg

1. Kreuze die richtige Antwort an

c
\alpha
W
\gamma
Länge [AB]
\beta

Punkte: 0 / 0


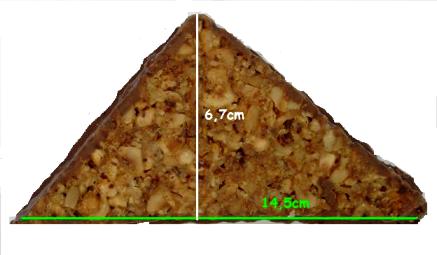
Aufgabe 3: Nussecke backen

Ebert Nussecke.jpg
Maja hat 30 Nussecken gebacken und möchte deren Oberseite vollständig mit Schokolade überziehen. Das Bild zeigt eine Nussecke, die 6,7 cm hoch und 14,5 cm breit ist. Alle Nussecken sind gleich groß.
Frage: Für welche Fläche braucht Maja Schokolade?

Sie benötigt für eine Fläche von 1457,25 ( nur die Zahl eintragen!) cm² Schokolade

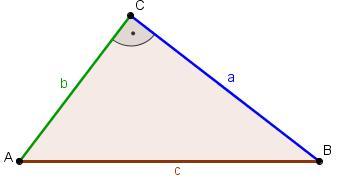
Aufgabe 4: Variation Dreieck

Wie sieht die Flächeninhaltsformel für ein...
  • ...rechtwinkliges Dreieck ABC aus?
Der rechte Winkel befindet sich am Eckpunkt C
Ebert rechtwinklig.jpg

1. Zu welchem speziellen Parallelogramm kann man das Dreieck ganz einfach ergänzen?

Man kann das Dreieck zu einem Parallelogramm mit der Seitenlänge c und der Höhe h ergänzen.
Man kann das Dreieck zu einem Rechteck mit der Seitenlänge c und der Breite a ergänzen.
Das Dreieck lässt sich zu einem Quadrat mit der Seitenlänge c ergänzen.

Punkte: 0 / 0



Ergänze die fehlenden Felder und ermittle daraus die Flächeninhaltsformel für das rechtwinklige Dreieck:

Bei der Ergänzung gilt z.B.:
Seite c im Dreieck = Länge c im Rechteck
Seite a im Dreieck = Breite a im Rechteck

Das rechtwinklige Dreieck ist halb so groß wie das entstehende Rechteck, daher gilt: Frechtwinklig = {1 \over 2} \cdot c \cdot a


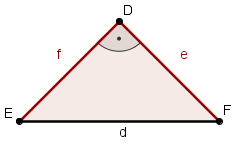
Wie sieht die Flächeninhaltsformel für ein...
  • ..gleichschenklig-rechtwinkliges Dreieck ABC aus?
Der rechte Winkel befindet sich am Eckpunkt C.
Ebert gleichschenklig.jpg

1. Zu welchem speziellen Parallelogramm kann man das Dreieck ganz einfach ergänzen?

Man kann das Dreieck zu einem Parallelogramm mit der Seitenlänge c und der dazugehörigen Höhe h ergänzen.
Man kann das Dreieck zu einem Rechteck mit der Länge c und der Breite a ergänzen.
Das Dreieck lässt sich zu einem Quadrat mit der Seitenlänge a ergänzen.

Punkte: 0 / 0
Ergänze die fehlenden Felder und ermittle daraus die Flächeninhaltsformel für das gleichschenklig-rechtwinklige Dreieck:

Bei der Ergänzung gilt z.B.:
Seite c im Dreieck = Seite c im Quadrat
Seite a im Dreieck = Seite a im Quadrat
Im Quadrat gilt: a = c


Das rechtwinklige Dreieck ist halb so groß wie das entstehende Quadrat, daher gilt:
Fgleichschenklig-rechtwinklig = {1 \over 2} \cdot a \cdot a = a²

Vertiefen und Erweitern zum Flächeninhalt des Dreiecks

Von „http://dmuw.zum.de/index.php?title=Übungsaufgaben_zur_Flächenberechnung_am_Dreieck&oldid=3541“