Übungsaufgaben zur Flächenberechnung am Dreieck: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 4: Wie ändert sich der Flächeninhalt im Dreieck?: applet eingefügt)
(Lob und Feedback)
Zeile 1: Zeile 1:
 
__NOTOC__
 
__NOTOC__
 
===Aufgabe 1===
 
===Aufgabe 1===
−
'''Berechne den Flächeninhalt der Dreiecke <span style="color: red">TIM</span>,  <span style="color: green">EVA</span> und <span style="color: blue ">RON</span>'''
+
'''''Berechne den Flächeninhalt der Dreiecke <span style="color: red">TIM</span>,  <span style="color: green">EVA</span> und <span style="color: blue ">RON</span>'''''
 
[[Bild:Ebert_DreieckeAufgabe2.jpg|center]]
 
[[Bild:Ebert_DreieckeAufgabe2.jpg|center]]
  
Zeile 13: Zeile 13:
  
 
===Aufgabe 2: Wovon hängt der Flächeninhalt ab?===
 
===Aufgabe 2: Wovon hängt der Flächeninhalt ab?===
−
Bestimme, wovon der Flächeninhalt des darsgestellten Dreiecks abhängt.  
+
'''''Bestimme, wovon der Flächeninhalt des dargestellten Dreiecks abhängt.'''''
  
 
[[Bild:Ebert_DreieckFrage.jpg|center]]
 
[[Bild:Ebert_DreieckFrage.jpg|center]]
Zeile 29: Zeile 29:
 
===Aufgabe 3: Nussecke backen===
 
===Aufgabe 3: Nussecke backen===
 
[[Bild:Ebert_Nussecke.jpg|center]]
 
[[Bild:Ebert_Nussecke.jpg|center]]
−
:'''Maja hat 30 Nussecken gebacken und möchte deren Oberseite vollständig mit Schokolade überziehen. Das Bild zeigt eine Nussecke, die 6,7 cm hoch und 14,5 cm breit ist. Alle Nussecken sind gleich groß. <br>
+
:'''''Maja hat 30 Nussecken gebacken und möchte deren Oberseite vollständig mit Schokolade überziehen. Das Bild zeigt eine Nussecke, die 6,7 cm hoch und 14,5 cm breit ist. Alle Nussecken sind gleich groß.''''' <br>
−
:'''''Frage:''''' Für welche Fläche braucht Maja Schokolade?'''
+
:'''''Frage:''''' '''''Für welche Fläche braucht Maja Schokolade?'''''
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
  
Zeile 36: Zeile 36:
  
 
</div>
 
</div>
 +
[[Bild:Ebert_Maja.jpg|200px]]
  
 
===Aufgabe 4: Wie ändert sich der Flächeninhalt im Dreieck? ===
 
===Aufgabe 4: Wie ändert sich der Flächeninhalt im Dreieck? ===
 +
<div style="border: 2px  solid blue; background-color:#ffffff; padding:7px;">
 +
{|
  
−
<ggb_applet height="400" width="400" showResetIcon="true" filename="Ebert_Dreieckvariieren.ggb" />
+
|<ggb_applet height="400" width="400" showResetIcon="true" filename="Ebert_Dreieckvariieren.ggb" />||
 
'''''Wie ändert sich der Flächeninhalt im Dreieck, wenn'''''<br>
 
'''''Wie ändert sich der Flächeninhalt im Dreieck, wenn'''''<br>
 
<quiz display="simple">
 
<quiz display="simple">
−
{...die Länge der '''<span style="color: green">Grundseite verdoppelt</span>''' wird und man die Höhe halbiert?}
+
{...d'''ie Länge der '''<span style="color: green">Grundseite verdoppelt</span>''' wird und man die <span style="color: blue">Höhe</span> halbiert?'''}
 
- Der Flächeninhalt wird '''verdoppelt'''
 
- Der Flächeninhalt wird '''verdoppelt'''
 
- Der Flächeninhalt wird '''vervierfacht'''
 
- Der Flächeninhalt wird '''vervierfacht'''
Zeile 49: Zeile 52:
 
- Der Flächeninhalt wird '''geviertelt'''
 
- Der Flächeninhalt wird '''geviertelt'''
  
−
{...eine '''<span style="color: blue">Höhe</span>''' verdopelt wird?}
+
{'''...eine '''<span style="color: blue">Höhe</span>''' verdoppelt wird?'''}
 
+ Der Flächeninhalt wird '''2 mal  so groß'''
 
+ Der Flächeninhalt wird '''2 mal  so groß'''
 
- Der Flächeninhalt wird '''4 mal so groß'''
 
- Der Flächeninhalt wird '''4 mal so groß'''
Zeile 55: Zeile 58:
 
- Der Flächeninhalt wird '''<math> {1\over 4} </math> mal so groß'''
 
- Der Flächeninhalt wird '''<math> {1\over 4} </math> mal so groß'''
  
−
{...wenn die Grundseite verdoppelt und die Höhe verdreifacht wird?}
+
{'''...wenn die <span style="color: green">Grundseite verdoppelt</span>  und die <span style="color: blue">Höhe verdreifacht</span> wird?'''}
 
- Der Flächeninhalt wird '''2 mal so groß'''
 
- Der Flächeninhalt wird '''2 mal so groß'''
 
- Der Flächeninhalt wird '''4 mal so groß'''
 
- Der Flächeninhalt wird '''4 mal so groß'''
Zeile 62: Zeile 65:
  
 
</quiz>
 
</quiz>
 +
''0-1 Punkt: Bearbeite die Aufgabe bitte nochmals'' <br>
 +
''2 Punkte: Das hast Du schon sehr gut gemacht! Weiter so.<br>''
 +
''3 Punkte: Prima! Du bist sehr gut!!''
  
 +
[[Bild:Ebert_Loballgemein.jpg|200px]]
 +
|}
 +
</div>
 +
 +
----
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
  
 +
===Get more and explore===
 +
[[Bild:Ebert_Motivatoren.jpg| 200px]]
 +
'''''Für die ganz Schnellen gibt es eine weitere Seite. Entdecke hier Spannendes zum Flächeninhalt des Dreiecks'''''
  
−
[[Vertiefen und Erweitern zum Flächeninhalt des Dreiecks]]
+
→[[Vertiefen und Erweitern zum Flächeninhalt des Dreiecks]]

Version vom 16. Juli 2009, 11:13 Uhr

Aufgabe 1

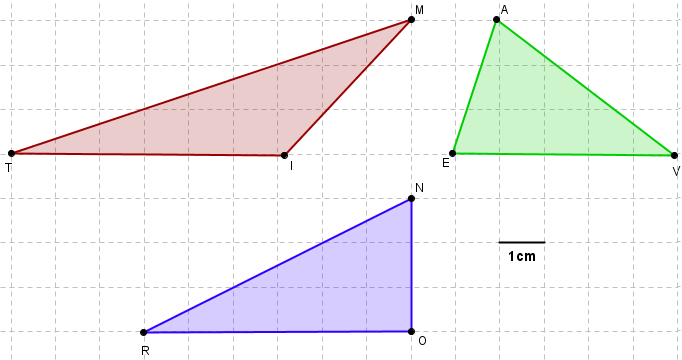
Berechne den Flächeninhalt der Dreiecke TIM, EVA und RON

Ebert DreieckeAufgabe2.jpg

Suche eine geeignete Grundseite und die dazugehörige Höhe!

Der Flächeninhalt von RON ist 7,5 (cm²)
Der Flächeninhalt von TIM ist 9 (cm²)
Der Flächeninhalt von EVA beträgt 7,5 (cm²)

Aufgabe 2: Wovon hängt der Flächeninhalt ab?

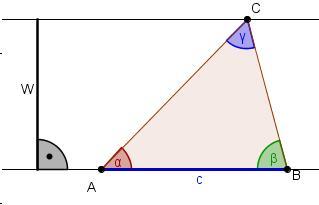
Bestimme, wovon der Flächeninhalt des dargestellten Dreiecks abhängt.

Ebert DreieckFrage.jpg

1. Kreuze die richtige Antwort an

c
\alpha
W
\gamma
Länge [AB]
\beta

Punkte: 0 / 0


Aufgabe 3: Nussecke backen

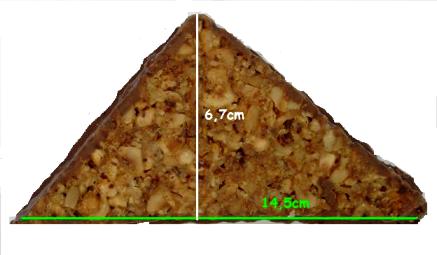
Ebert Nussecke.jpg
Maja hat 30 Nussecken gebacken und möchte deren Oberseite vollständig mit Schokolade überziehen. Das Bild zeigt eine Nussecke, die 6,7 cm hoch und 14,5 cm breit ist. Alle Nussecken sind gleich groß.
Frage: Für welche Fläche braucht Maja Schokolade?

Sie benötigt für eine Fläche von 1457,25 ( nur die Zahl eintragen!) cm² Schokolade

Ebert Maja.jpg

Aufgabe 4: Wie ändert sich der Flächeninhalt im Dreieck?

Wie ändert sich der Flächeninhalt im Dreieck, wenn

1. ...die Länge der Grundseite verdoppelt wird und man die Höhe halbiert?

Der Flächeninhalt wird verdoppelt
Der Flächeninhalt wird vervierfacht
Der Flächeninhalt bleibt gleich
Der Flächeninhalt wird halbiert
Der Flächeninhalt wird geviertelt

2. ...eine Höhe verdoppelt wird?

Der Flächeninhalt wird 2 mal so groß
Der Flächeninhalt wird 4 mal so groß
Der Flächeninhalt wird {1\over 2} mal so groß
Der Flächeninhalt wird {1\over 4} mal so groß

3. ...wenn die Grundseite verdoppelt und die Höhe verdreifacht wird?

Der Flächeninhalt wird 2 mal so groß
Der Flächeninhalt wird 4 mal so groß
Der Flächeninhalt wird 6 mal so groß
Der Flächeninhalt wird 5 mal so groß

Punkte: 0 / 0

0-1 Punkt: Bearbeite die Aufgabe bitte nochmals
2 Punkte: Das hast Du schon sehr gut gemacht! Weiter so.
 3 Punkte: Prima! Du bist sehr gut!!

Ebert Loballgemein.jpg







Get more and explore

Ebert Motivatoren.jpg Für die ganz Schnellen gibt es eine weitere Seite. Entdecke hier Spannendes zum Flächeninhalt des Dreiecks

→Vertiefen und Erweitern zum Flächeninhalt des Dreiecks

Von „http://dmuw.zum.de/index.php?title=Übungsaufgaben_zur_Flächenberechnung_am_Dreieck&oldid=3607“