Flächeninhalt ebener Figuren: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(Lob)
(→‎Das solltest Du wissen: Formel mit Erklärung eingefügt)
Zeile 45: Zeile 45:
 
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
 
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
 
{| <br>
 
{| <br>
−
| [[Bild:Ebert_MotivatorMerke.jpg]]||
+
| [[Bild:Ebert_MotivatorMerke.jpg|200px]]||
−
Den <span style="color: red">'''Flächeninhalt von Rechtecken'''</span> berechnet man durch die folgende Formel:<br>
+
*<u>Den <span style="color: red">'''Flächeninhalt von Rechtecken'''</span> berechnet man durch die Formel:</u><br>
 
::::<math>F_{Rechteck}= g \cdot b</math>
 
::::<math>F_{Rechteck}= g \cdot b</math>
 
<br>
 
<br>
−
mit <span style="color: red">'''g'''</span> als der <span style="color: red">'''Länge der Grundseite'''</span> und <span style="color: red">'''b als Breite'''</span> des Rechteckes.
+
:mit <span style="color: red">'''g'''</span> als <span style="color: red">'''Länge der Grundseite'''</span> und <span style="color: red">'''b als Breite'''</span> des Rechtecks.
 
<br>
 
<br>
 
<br>
 
<br>
−
Analog berechnet sich der <span style="color: red">'''Flächeninhalt von Quadraten'''</span> durch:<br>
+
*<u>Ebenso berechnet man den <span style="color: red">'''Flächeninhalt von Quadraten'''</span>:</u>
−
::::<math>F_{Quadrat} = a\cdot a = a^2 </math>
+
::::<math>F_{Quadrat} = g\cdot b </math> <br>
 +
::::Doch <span style="color: red">'''im Quadrat sind die Seiten b und g gleich lang'''</span>! <br>
 +
::::Das heißt wir können schreiben: <br>
 +
:::<math>F_{Quadrat} = g\cdot g = g^2</math> <math>oder</math>  <math>F_{Quadrat} = b\cdot b = b^2</math>. <br>
 +
 
 +
 
 
<br>
 
<br>
−
mit <span style="color: red">'''a als Seitenlänge'''</span> des Quadrates.
+
 
 
|}
 
|}
 
</div>
 
</div>

Version vom 22. Juli 2009, 18:43 Uhr


1.Wiederholung: Flächeninhalt von Rechtecken und Quadraten

Entdecke auf dieser Seite, wie man die Flächeninhalte ebener Figuren berechnet!!
Ebert MotivatorenRechteck.jpg


Du hast bereits gelernt, wie man den Flächeninhalt von Rechtecken und Quadraten berechnet.
Erinnerst Du Dich noch daran?




Teste Dich in der nächsten Aufgabe. Berechne die fehlenden Felder und fülle die Lücken mit der passenden Antwort aus.


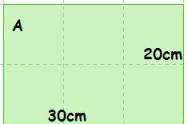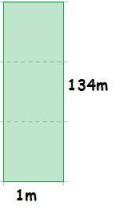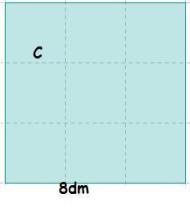Ebert RechteckA.jpg 30cm \cdot                     = 600                    Ebert RechteckB.jpg 1m \cdot 134m =                     Ebert RechteckC.jpg                     \cdot 8dm = 64                   
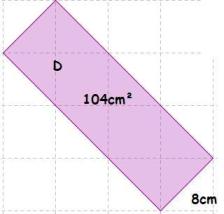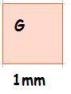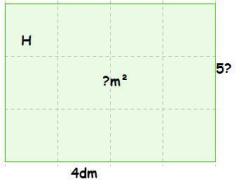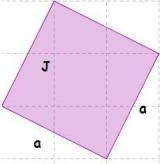Ebert RechteckD.jpg 8cm \cdot                     cm = 104cm2 Ebert RechteckG.jpg 1mm \cdot 1mm=                     Ebert RechteckH.jpg 4dm \cdot 5                    =                     m2 Ebert RechteckI.jpg a \cdot                     = ab Ebert RechteckJ.jpg a \cdot a =                    

cm28dm134m 2b20cmdm 2a21mm213m2


Ebert MotivatorRot.jpg

Du hast alle Aufgabe richtig gelöst? Sehr gut!
Dann kennst Du noch die Flächeninhaltsformel für Rechtecke und Quadrate.
Überprüfe im nächsten Abschnitt, ob du richtig liegst.






Das solltest Du wissen


Merke Dir die Berechnung für die Flächeninhalte des Rechtecks und Quadrates gut! Du wirst sie später wieder gebrauchen.


Ebert MotivatorMerke.jpg
  • Den Flächeninhalt von Rechtecken berechnet man durch die Formel:
F_{Rechteck}= g \cdot b


mit g als Länge der Grundseite und b als Breite des Rechtecks.



  • Ebenso berechnet man den Flächeninhalt von Quadraten:
F_{Quadrat} = g\cdot b
Doch im Quadrat sind die Seiten b und g gleich lang!
Das heißt wir können schreiben:
F_{Quadrat} = g\cdot g = g^2 oder F_{Quadrat} = b\cdot b = b^2.




Ebert Motivatoren.jpg Das war doch ganz leicht,oder?
Konzentrier Dich im nächsten Abschnitt gut, denn da lernst Du wieder etwas Neues.

Hier geht es weiter zum nächsten Abschnitt:
→Flächeninhalt Parallelogramm

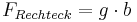
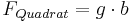
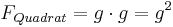
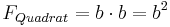Von „http://dmuw.zum.de/index.php?title=Lernpfade/Flächeninhalt_ebener_Figuren/Flächeninhalt_ebener_Figuren&oldid=3865“