Variation am Dreieck: Unterschied zwischen den Versionen

Version vom 17. August 2009, 13:40 Uhr

Variation am Dreieck

Gegeben sind die Seiten:
a =3cm, b= 4cm und c = 5cm

Zeig Maja´s Überlegung an

Ist nicht schon eine Höhe gegeben? Zeig den Hinweis von Nils an

'

Welches spezielle Dreieck ist das Dreieck ABC?

Brauchst Du den Hinweis?
[Anzeigen][Verstecken]

Dreieck ABC ist rechtwinklig

Maja hat eine Lösung gefunden

[Anzeigen][Verstecken]

Die Seiten a und b des Dreiecks ABC sind gleichzeitig auch Grundseite und Höhe, da das Dreieck ABC rechtwinklig ist und somit a senkrecht zu b ist.

Es gilt zum Beispiel:

Seite b ist Grundseite, damit ist die Länge der Grundseite b 4 (cm)

Die Seite a wird damit zur Höhe und da: a = 3 cm

ist der Flächeninhalt des Dreiecks 6(cm²)

Nils hat die Formel für die Berechnung dieses speziellen Dreiecks zusammengefasst:

Der Flächeninhalt eines rechtwinkligen Dreiecks berechnet sich durch :

F_rechtwinklig = ${1 \over 2}$ $\cdot$ b $\cdot$ a

wobei die Seiten a und b senkrecht zueinander stehen.

Wie lautet die Flächeninhaltsformel für ein

..gleichschenklig-rechtwinkliges Dreieck EFD ?

Der rechte Winkel befindet sich am Eckpunkt D.

Ergänze die fehlenden Felder und ermittle daraus die Flächeninhaltsformel für das gleichschenklig-rechtwinklige Dreieck:

1. Flächeninhaltsformel des rechtwinkligen Dreiecks:

F_rechtwinklig = ${1 \over 2}$ $\cdot$ e $\cdot$ f

2. Im gleichschenkligen Dreieck gilt für die Seiten f und e:

f = e

$\Rightarrow$ Für den Flächeninhalt F eines rechtwinkligen und gleichschenkligen Dreiecks gilt:
F = ${1 \over 2}$ $\cdot$ e $\cdot$ e = ${1 \over 2}$ $\cdot$ e²

Flächeninhalt von stumpfwinkligen Dreiecken

Ziehe den roten Eckpunkt C zu auf die Punkte D, E und F.

Begründe Deine Antwort!

Man kann also in einem Dreieck den der Grundseite gegenüberliegenden Punkt auf einer Parallelen zur Grundseite wandern lassen, ohne dass sich dabei der Flächeninhalt des Dreiecks ändert.
Grundseite und Höhe bleiben dabei immer gleich, also auch der Flächeninhalt.
Diesen Bewegungsvorgang nennt man Scherung. Du hast dieses Prinzip bereits bei den Parallelogrammen kennen gelernt.

Spitze! Du hast die Aufgabe prima bearbeitet

→Übungsaufgaben zur Flächenberechnung am Dreieck

Hier geht es zurück zur Seite: Zusammenfassung: Flächeninhalt des Dreiecks

@@ Zeile 55: / Zeile 55: @@
 ====Wie lautet die Flächeninhaltsformel für ein====
-:'''..gleichschenklig-rechtwinkliges Dreieck ABC ?'''
+:'''..gleichschenklig-rechtwinkliges Dreieck EFD ?'''
 :'''Der rechte Winkel befindet sich am Eckpunkt D.'''''
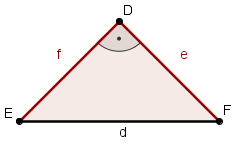
 [[Bild:Ebert_gleichschenklig.jpg|center]]
-<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
+<div style="border: 2px solid green; background-color:#ffffff; padding:7px;">
 {|
 '''''Ergänze die fehlenden Felder und ermittle daraus die Flächeninhaltsformel für das gleichschenklig-rechtwinklige Dreieck:'''''

Variation am Dreieck: Unterschied zwischen den Versionen

Version vom 17. August 2009, 13:40 Uhr