Prinzipielle Grenzen der Berechenbarkeit: Unterschied zwischen den Versionen
K (→Gödelisierung) |
K (→Gödelisierung) |
||
| Zeile 37: | Zeile 37: | ||
Wir versuchen jetzt Hilfe von der Mathematik zu erhalten. Dazu wandelt man Probleme in eine Form um, die es erlaubt, Wissen über Abbildungen innerhalb der natürlichen Zahlen zu benutzen. | Wir versuchen jetzt Hilfe von der Mathematik zu erhalten. Dazu wandelt man Probleme in eine Form um, die es erlaubt, Wissen über Abbildungen innerhalb der natürlichen Zahlen zu benutzen. | ||
| − | + | Um dies zu erreichen, wandelt man die Ein- und Ausgabedaten in natürliche Zahlen um. Dies kann mehr oder minder geschickt erfolgen. Kurt Gödel hat sich mit solchen Fragestellungen beschäftigt, weshalb man entsprechende Verfahren '''Gödelisierungen''' nennt.. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{{Aufgabe-Mathe| | {{Aufgabe-Mathe| | ||
| Zeile 87: | Zeile 79: | ||
}} | }} | ||
| + | |||
| + | Mit der Gödelisierung lassen sich beliebige Eingabedaten in natürliche Zahlen umwandeln. Diese Vorgehensweise wird häufig in der theoretischen Informatik verwendet, da sich Algorithmen dadurch auf Funktionen über den natürlichen Zahlen abbilden lassen. Dafür gibt es verschiedenste Verfahren. Man fasst solch ein Verfahren als Abbildung <math>g</math> von der Menge der Programme <math>M</math> in die Menge der natürlichen Zahlen <math>\mathbb{N}</math> auf: <math>g: M \rightarrow \mathbb{N}</math>. | ||
| + | Die Abbildung muss dabei noch drei Bedingungen erfüllen: | ||
| + | |||
| + | * <math>g</math> muss injektiv sein, d.h. jede natürliche Zahl darf höchstens das Bild von einem Programm sein; aber nicht jede natürliche Zahl muss auch ein Programm sein | ||
| + | * Die Bildmenge muss entscheidbar sein, es muss also einen Algorithmus der Ja ausgibt, wenn die Zahl einem Programm entspricht und Nein, wenn es sich um kein Programm handelt. | ||
| + | * Die Umkehrfunktion <math>g^{-1}</math> muss berechenbar sein, d.h. man muss aus der natürlichen Zahl auch wieder das Programm bekommen können. | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
Version vom 25. September 2009, 09:31 Uhr
Inhaltsverzeichnis |
Abzählbarkeit
30px Merke
Eine Menge |
Beispiele für abzählbare Mengen:
- die Menge der natürlichen Zahlen
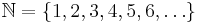
- die Primzahlen
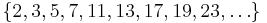
- die Menge der ganzen Zahlen
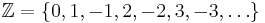
- jede Menge mit endlich vielen Elementen
- die Menge der rationalen Zahlen
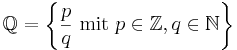 (= die Menge aller Brüche)
(= die Menge aller Brüche)
Beispiele für nicht abzählbare Mengen:
- die Menge der reellen Zahlen
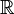
- die Potenzmenge der natürlichen Zahlen
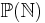 , also die Menge aller Teilmengen der natürlichen Zahlen
, also die Menge aller Teilmengen der natürlichen Zahlen
Programme sind eine endliche Folge von Wörtern über einem endlichen Alphabet (in der Praxis meist der ASCII-Code). Schreibt man den kompletten Programmtext in eine Zeile, so kann man die einzelnen Programme zunächst der Länge nach ordnen. Innerhalb der Programme einer festen Länge ordnet man diese lexikographisch, d.h. wie in einem Telefonbuch. Damit kann man folgern, dass die Menge der Programme abzählbar ist.
Aufzählbarkeit
Entscheidbarkeit
Berechenbarkeit
Gödelisierung
Wir versuchen jetzt Hilfe von der Mathematik zu erhalten. Dazu wandelt man Probleme in eine Form um, die es erlaubt, Wissen über Abbildungen innerhalb der natürlichen Zahlen zu benutzen. Um dies zu erreichen, wandelt man die Ein- und Ausgabedaten in natürliche Zahlen um. Dies kann mehr oder minder geschickt erfolgen. Kurt Gödel hat sich mit solchen Fragestellungen beschäftigt, weshalb man entsprechende Verfahren Gödelisierungen nennt..
|
Die 26 Buchstaben des Alphabets werden mit den Zahlen 1 bis 26 kodiert. Damit könnte man ein geschriebenes Wort als Zahl schreiben. Dekodiere die Zahl "26235945212097"! Welche Buchstabenfolge erhält man nach dem Dekodieren?
Möglichkeiten für das dekodierte Wort sind z.B.: ZWEIDEUTIG oder BFBCEIDEBATIG oder ...
|
|
Nun werden die 26 Buchstaben des Alphabets wie folgt kodiert: Den 26 Buchstaben des Alphabets wird jeweils eine eindeutige Zahl zwischen 1 und 26 zugeordnet. Ein Wort wird nun mit fortlaufenden Primzahlpotenzen kodiert, also wenn a die Zahl 1, b die Zahl 2, c die Zahl 3 zugeordnet wird, dann wird das Wort abbca wie folgt kodiert:
Multipliziert man diese Zahlen miteinander, erhält man die Zahl
Das dekodierte Wort lautet: INFORMATIK. Dies Art der Kodierung ist eher von theoretischer Bedeutung, weil man sehr schnell gigantisch große Zahlen erhält. Es ist auch ziemlich aufwändig diese Zahlen in Primfaktoren zu zerlegen. Aus diesem Grund sind große Primzahlen für die Verschlüsselungstechnik so wichtig.
|
|
Nun werden die 26 Buchstaben des Alphabets mit den Zahlen 01 bis 26 kodiert. Schreibt man die kodierten Buchstaben hintereinander, so erhält man eine Zahl. Dekodiere die Zahl 26230509060512121519.
Das dekodierte Wort lautet: ZWEIFELLOS
|
Mit der Gödelisierung lassen sich beliebige Eingabedaten in natürliche Zahlen umwandeln. Diese Vorgehensweise wird häufig in der theoretischen Informatik verwendet, da sich Algorithmen dadurch auf Funktionen über den natürlichen Zahlen abbilden lassen. Dafür gibt es verschiedenste Verfahren. Man fasst solch ein Verfahren als Abbildung 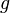 von der Menge der Programme
von der Menge der Programme 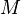 in die Menge der natürlichen Zahlen
in die Menge der natürlichen Zahlen 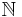 auf:
auf: 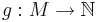 .
Die Abbildung muss dabei noch drei Bedingungen erfüllen:
.
Die Abbildung muss dabei noch drei Bedingungen erfüllen:
-
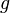 muss injektiv sein, d.h. jede natürliche Zahl darf höchstens das Bild von einem Programm sein; aber nicht jede natürliche Zahl muss auch ein Programm sein
muss injektiv sein, d.h. jede natürliche Zahl darf höchstens das Bild von einem Programm sein; aber nicht jede natürliche Zahl muss auch ein Programm sein
- Die Bildmenge muss entscheidbar sein, es muss also einen Algorithmus der Ja ausgibt, wenn die Zahl einem Programm entspricht und Nein, wenn es sich um kein Programm handelt.
- Die Umkehrfunktion
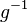 muss berechenbar sein, d.h. man muss aus der natürlichen Zahl auch wieder das Programm bekommen können.
muss berechenbar sein, d.h. man muss aus der natürlichen Zahl auch wieder das Programm bekommen können.
Welches der obigen Verfahren eignet sich für eine Gödelisierung? (!Kodierung mit Zahlen 1 bis 26) (Kodierung mit Zahlen 01 bis 26) (Kodierung mit Primzahlpotenzen)(!Keines der Verfahren)
Fleißige Biber
Halte-Problem
|
Die Schüler der Kollegstufe besuchen |
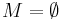 ) oder es eine Funktion
) oder es eine Funktion 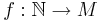 gibt, die surjektiv ist (jedes Element aus
gibt, die surjektiv ist (jedes Element aus 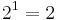 kodiert.
kodiert.
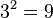 kodiert.
kodiert.
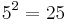 kodiert.
kodiert.
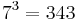 kodiert.
kodiert.
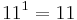 kodiert.
kodiert.
 .
Da die Primfaktorzerlegung eindeutig ist, wenn man die Primzahlpotenzen aufsteigend ordnet, kann man aus jeder Zahl das zugehörige Wort erzeugen.
Welche Buchstabenfolge erhält man, wenn man die Zahl
.
Da die Primfaktorzerlegung eindeutig ist, wenn man die Primzahlpotenzen aufsteigend ordnet, kann man aus jeder Zahl das zugehörige Wort erzeugen.
Welche Buchstabenfolge erhält man, wenn man die Zahl 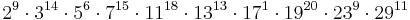 dekodiert?
dekodiert?
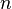 verschiedene Kurse. Jeder Kurs findet einmal pro Woche statt. Belegt ein Schüler zwei Kurse, so dürfen diese nicht gleichzeitig stattfinden. Kann man mit
verschiedene Kurse. Jeder Kurs findet einmal pro Woche statt. Belegt ein Schüler zwei Kurse, so dürfen diese nicht gleichzeitig stattfinden. Kann man mit 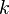 verschiedenen Terminen auskommen?
Erstelle hierzu eine Graphen, wobei ein Knoten einem Kurs entspricht. Zwei Knoten werden genau dann miteinander verbunden, wenn ein Schüler die beiden entsprechenden Kurse besucht.
Man kann die Aufgabe als sogenanntes
verschiedenen Terminen auskommen?
Erstelle hierzu eine Graphen, wobei ein Knoten einem Kurs entspricht. Zwei Knoten werden genau dann miteinander verbunden, wenn ein Schüler die beiden entsprechenden Kurse besucht.
Man kann die Aufgabe als sogenanntes 
