Berechenbarkeit: Unterschied zwischen den Versionen
K |
|||
| Zeile 10: | Zeile 10: | ||
{{Lernpfad| | {{Lernpfad| | ||
| − | ===[[/ | + | ===[[/Lernpfad_theoretische_Berechenbarkeit/]]=== |
Es werden folgende Begriffe behandelt: | Es werden folgende Begriffe behandelt: | ||
| − | |||
| − | |||
| − | |||
| − | |||
* Algorithmus | * Algorithmus | ||
* Gödelisierung | * Gödelisierung | ||
| + | * Turing-Maschine | ||
| + | * Churchsche These | ||
* Halteproblem | * Halteproblem | ||
| + | * Fleißige Biber | ||
}} | }} | ||
{{Lernpfad| | {{Lernpfad| | ||
| − | ===[[/Lernpfad | + | ===[[/Lernpfad praktische Berechenbarkeit/]]=== |
Es werden folgende Begriffe behandelt: | Es werden folgende Begriffe behandelt: | ||
* Effizienz | * Effizienz | ||
Version vom 27. September 2009, 22:55 Uhr
Benutzer: Matthias Häufglöckner
Personenbeschreibung:
Julius-Maximilians-Universität Würzburg
Student für ein Lehramt an Gymnasien
Fächerkombination: Mathematik/Informatik
Dieser Lernpfad wird im Rahmen einer Zulassungsarbeit in der Didaktik der Informatik erstellt.
Betreuender Dozent: Michael Schuster
|
Lernpfad
|
|
Lernpfad
|
Probleme:
- Rendering von MathML uneinheitlich
- Vorlagen und div inkompatibel
- Zuordnungsquiz mit Formeln lassen sich bei einigen Browsern nach falscher Eingabe nicht mehr ziehen.
- Bei der Vorlage Lösung versteckt kann man keine Tabellen benutzen
Temporär
|
Die Schüler der Kollegstufe besuchen |
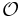 -Notation
-Notation
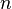 verschiedene Kurse. Jeder Kurs findet einmal pro Woche statt. Belegt ein Schüler zwei Kurse, so dürfen diese nicht gleichzeitig stattfinden. Kann man mit
verschiedene Kurse. Jeder Kurs findet einmal pro Woche statt. Belegt ein Schüler zwei Kurse, so dürfen diese nicht gleichzeitig stattfinden. Kann man mit 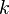 verschiedenen Terminen auskommen?
Erstelle hierzu eine Graphen, wobei ein Knoten einem Kurs entspricht. Zwei Knoten werden genau dann miteinander verbunden, wenn ein Schüler die beiden entsprechenden Kurse besucht.
Man kann die Aufgabe als sogenanntes
verschiedenen Terminen auskommen?
Erstelle hierzu eine Graphen, wobei ein Knoten einem Kurs entspricht. Zwei Knoten werden genau dann miteinander verbunden, wenn ein Schüler die beiden entsprechenden Kurse besucht.
Man kann die Aufgabe als sogenanntes 
