Volumen des Zylinders: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(1. Aufgabe) |
|||
| Zeile 3: | Zeile 3: | ||
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
==1. Aufgabe== | ==1. Aufgabe== | ||
| − | Wir haben im ersten Lernpfad dreiseitige Prismen wiederholt. Dort haben wir auch festgestellt, dass die Formel für das Volumen eines Körpers in der Grundform immer gleich ist, nämlich <math>V=G\cdot h_K</math>. Diese Formle gilt ebenso für unseren neune Körper Zylinder. | + | <div class="lueckentext-quiz"> |
| − | Nun benötigen wir aber noch die Grundfläche G. Diese besteht bei unserem Zylinder aus einem Kreis. Der Flächeninhalt des Kreises lässt sich mit <math>A=r^2\cdot \pi</math> darstellen. | + | Wir haben im ersten Lernpfad dreiseitige '''Prismen''' wiederholt. Dort haben wir auch festgestellt, dass die Formel für das '''Volumen''' eines Körpers in der Grundform immer gleich ist, nämlich '''<math>V=G\cdot h_K</math>'''. Diese Formle gilt ebenso für unseren neune Körper '''Zylinder'''. |
| − | Also können wir die Formel für das Zylindervolumen zusammenfügen: <math>V=G\cdot h_K=r^2\cdot \pi\cdot h_K</math>. | + | Nun benötigen wir aber noch die '''Grundfläche''' G. Diese besteht bei unserem Zylinder aus einem '''Kreis'''. Der '''Flächeninhalt''' des Kreises lässt sich mit '''<math>A=r^2\cdot \pi</math>''' darstellen. |
| + | Also können wir die Formel für das '''Zylindervolumen''' zusammenfügen: <math>V=G\cdot h_K=r^2\cdot \pi\cdot h_K</math>. | ||
| + | </div> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | </div> | ||
Version vom 23. November 2009, 11:15 Uhr
Hier werden wir uns nun um das Volumen des Zylinders kümmern. Du benötigst dafür dein Schulheft und Stifte
1. Aufgabe
Wir haben im ersten Lernpfad dreiseitige Prismen wiederholt. Dort haben wir auch festgestellt, dass die Formel für das Volumen eines Körpers in der Grundform immer gleich ist, nämlich 
. Diese Formle gilt ebenso für unseren neune Körper Zylinder.
Nun benötigen wir aber noch die Grundfläche G. Diese besteht bei unserem Zylinder aus einem Kreis. Der Flächeninhalt des Kreises lässt sich mit 
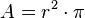darstellen.
Also können wir die Formel für das Zylindervolumen zusammenfügen: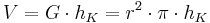 
.
