Der Satz des Thales: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(→‎Viel Spaß beim Multiple-Choice!)
(→‎Viel Spaß beim Multiple-Choice!)
Zeile 321: Zeile 321:
 
+ Der Winkel β misst immer 90°.
 
+ Der Winkel β misst immer 90°.
 
<br>
 
<br>
−
</quiz> || <ggb_applet height="350" width="550" showResetIcon="true" filename="KreuzwortThales_nicostahl.ggb" />
+
</quiz> || <ggb_applet height="350" width="600" showResetIcon="true" filename="KreuzwortThales_nicostahl.ggb" /> <br> <br> <ggb_applet height="350" width="600" showResetIcon="true" filename="ThalesKreuz_Nico.Stahl.ggb" />  
 
|}
 
|}
 
</div>
 
</div>

Version vom 10. Juni 2009, 15:04 Uhr


Mathematik-digital Pfeil-3d.png
Lernpfad

Der Satz des Thales

Nach dem griechischen Philosophen und Mathematiker Thales von Milet (um 600 v. Chr.) wird ein wichtiger gemeotrischer Satz bezeichnet.



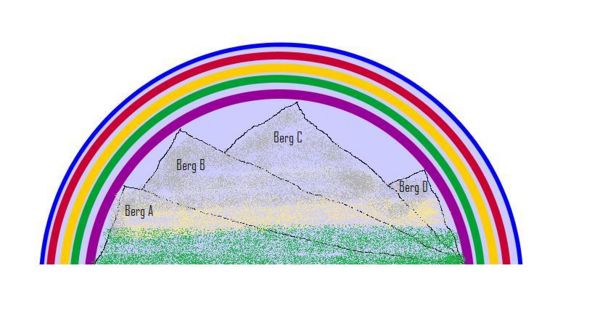
Hier siehst du einen schönen Regenbogen mitten in einer Berglandschaft auf dem Planet Phantasia.

Berglandschaft mit Regenbogen




Welcher Gipfel dieser Berglandschaft ist am spitzesten?

Frage a): Hast du eine Idee, wie groß der Winkel am Gipfel von Berg A sein könnte?

Antwort a): Der Berg A hat am Gipfel ein Winkelmaß von: 90°

Frage b): Haben die Winkel der Berge A,B,C,D, die den Regenbogen berühren eine Gemeinsamkeit?

Antwort b): Alle Winkel, die den Regenbogen berühren sind gleich groß.









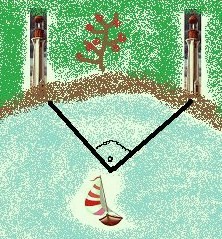
Ein Matrose und sein Kapitän segeln zusammen am Meeresufer entlang und entdecken zwei Leuchttürme unter einem Winkel von 90°.

Leuchttürme mt Segelschiff


Überlegungen:


  • Welche Position könnte denn das Segelschiff haben?


  • Stehen die beiden Leuchttürme zueinander in Beziehung?


  • Könnte es sich um eine geometrische Figur handeln, wenn man Objekte miteinander verbindet?


  • Was bedeutet die Angabe: "unter einem Winkel von 90°" Was kannst du daraus schließen?



Auf gehts - löse den Lückentext:

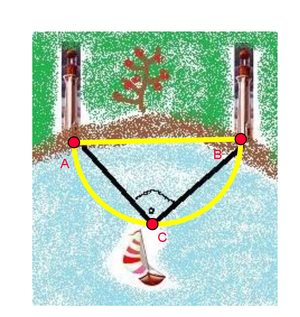
Zwei Standorte auf dem Festland werden mit A und B bezeichnet. In der Zeichnung sind das die Leuchttürme .
Das Objekt im Meer, also das Segelschiff wird mit dem Buchstaben C versehen. Nun verbinden wir die Punkte A,B und C miteinander und erhalten ein rechtwinkliges Dreieck.
Der Winkel an der Spitze C beträgt 90°.
Der Matrose und sein Kapitän segeln mit dem Schiff vom linken zum rechten Leuchtturm genau so, dass der Winkel bei C stets ein Maß von 90° hat.
Dies lässt vermuten, dass die gefahrene Route einen Halbkreis ergibt.
Den Mittelpunkt dieses Halbkreises bildet die Strecke AB .


















Anhand dieser Zeichnung kannst du den Zusammenhang erkennen, den du im Lückentext erarbeiten solltest.

Leuchttürme mit Segelschiff "Thales"



Frage a): Wenn das Schiff zum Leuchtturm B fährt, unter welchem Winkel blicken der Matrose und der Kapitän aufs Festland?

Antwort a): Die beiden Seeleute betrachten es von einem 90° Winkel aus.

Frage b): Wenn aber das Schiff zum Leuchtturm A fährt, unter welchem Winkel blicken dann die Schiffsleute aufs Festland ?

Antwort b): Dann betrachten es die Seemänner von einem 90° Winkel aus.


Daraus können wir schließen, dass der Winkel bei C immer rechtwinklig ist,
wenn die Strecke von Leuchtturm A zu Leuchtturm B der Durchmesser des Halbkreises über der Strecke AB ist.





Betrachte aufmerksam die dynamische Animation!

 Auf gehts - Löse das Quiz!



Beziehe dich dabei auf die nebenstehende Animation.


Wenn die Strecke AB den Mittelpunkt M des Kreises schneidet, dann erscheint im Bild das Wort Thales.
Weiterhin gilt dann auch, dass der Winkel an der Spitze C (grün markiert) rechtwinklig ist.
Wenn das Dreieck ABC bei C ein Maß von 90° hat, so bezeichnet man die Strecke AB als Hypotenuse.
Die beiden Strecken AC und BC nennt man Katheten.







Verwende den Schieberegler!

Was fällt dir beim Ziehen auf? Waagrecht und senkrecht, gefundene Wörter werden grün markiert.
Hier findest du Wörter, die du beim Bearbeiten des Lernpfades kennengelernt hast.
Hypotenuse
Dreieck
rechtwinklig
Thalessatz
Durchmesser
Radius
Kathete
Basiswinkel




Betrachte aufmerksam die dynamische Animation!



Versuche den Lückentext mithilfe der dynamischen Zeichnung zu lösen.


Wenn das Dreieck ABC bei dem Eckpunkt C rechtwinklig ist, dann liegt C auf dem Halbkreis über dem Durchmesser AB.
Wenn der Punkt C auf dem Halbkreis über AB liegt, dann ist das Dreieck ABC rechtwinklig bei C.

In der Mathematik kommt es häufig vor, dass Satz und Kehrsatz richtig sind.
Anstelle von zwei Sätzen in Wenn-Dann-Form, wird die Formulierung "...genau dann, wenn..." verwendet,
sowohl um die Sätze zusammenzufassen als auch um die Korrektheit der Aussage zu artikulieren.


Das Dreieck ABC hat genau dann bei C einen rechten Winkel, wenn die Ecke C auf dem Halbkreis über der Strecke AB liegt.





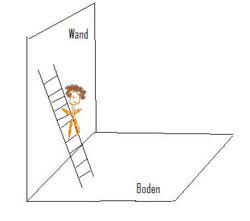
Die rutschende Leiter:

Ziehe an dem grünen Punkt B Anmerkungen und Arbeitsauftrag
Was fällt dir auf, wenn du am grünen Punkt B ziehst?
Der Satz des Thales findet Anwendung beim Lösen dieses Problems.
  Aufgabe   Stift.gif

Viel Spaß beim Tüfteln:

  • Stelle dir vor, eine Leiter (hier die Strecke AB) lehnt an einer Wand.
  • Die Person, die auf der Leiter steht, befindet sich exakt in der Mitte der Strecke AB.Leiterrutschend nicoStahl.jpg
  • Frage: Hast du eine Idee auf welchem geometrischen Ort sich die Person befindet, wenn die Leiter von der Wand abrutscht?
  • Hier hast du einen Lösungsvoschlag:Die rutschende Leiter

Weitere Informationen erhaltet ihr auch auf dieser Homepage:
 Die rutschende Leiter - Universität Bayreuth








Beweisführung für den Satz des Thales!

Klicke mit der linken Maustaste die einzelnen Schritte an.
Wenn du möchtest kannst du am Punkt C mit der Maus ziehen.



Auf gehts - löse den Lückentext:

Fülle die Lücken, indem du die passenden Begriffe zu den Feldern ziehst (mit der linken Maustaste zur Lücke ziehen und fallenlassen).


Wir wollen diesen Sachverhalt nun mathematisch untersuchen und dazu gehen wir davon aus,
dass das in der Zeichnung ersichtliche Dreieck einen rechten Winkel bei C aufzeigt.
Also sind die Punkte A, B und C gleich weit von M entfernt,
liegen somit auf dem Kreis um M,
der zugleich Mittelpunkt von der Strecke AB ist.
Das heißt, wenn das Dreieck ABC bei der Ecke C rechtwinklig ist,
dann liegt C auf dem Halbkreis über der Strecke AB.
Die Strecke AB ist zudem auch der Durchmesser des THALES-KREISES .























Hier lernst du den Widerspruchsbeweis kennen!

Ziehe an dem roten Punkt mit der linken Maustaste. Was fällt dir auf, wenn du das Kästchen "Punkt fixieren" anklickst?









Viel Spaß beim Multiple-Choice!


Lies die folgenden Sätze konzentriert durch und klicke die korrekten Aussagen mit der linken Maustaste an. Achte auf die Fragestellungen!!!

1. Welche dieser Aussagen über das Dreieck ABC ist wahr?

Die Summe aus den Winkeln α + β ergeben zusammen immer 60°.
Die Summe der beiden Winkel α + β ist immer gleich.
Das Maß des Winkels γ an der Spitze C berechnet sich aus der Summe der beiden Winkel α + β.
Der Winkel β kann nie doppelt so groß sein wie der Winkel α.
Der Winkel α misst immer 90°.
Der Winkel β misst immer 90°.
Der Winkel γ misst immer 90°.
Der Winkel γ misst nie 90°.
Falls gilt: α = 45°, so folgt: α = β.
Die beiden Winkel α und β sind nie maßgleich.

2. Welche dieser Aussagen über das Dreieck ABC ist falsch?

Der Winkel γ misst stets 90°.
Die zwei Winkel α und β haben niemals die gleiche Größe.
Addiert man die beiden Winkeln α + β zusammen, so erhält man stets 60°.
Das Maß des Winkels γ an der Spitze C berechnet sich aus der Summe der zwei Winkel α + β.
Der Winkel β kann nie doppelt so groß sein wie der Winkel α.
Der Winkel α misst immer 90°.
Die Summe der beiden Winkel α + β ist immer gleich.
Der Winkel γ misst nie 90°.
Falls gilt: α = 45°, so folgt: α = β.
α kann nie das Maß 45° haben.
Der Winkel β misst immer 90°.

Punkte: 0 / 0





Nuvola apps kig.png   Merke

Der Satz des Thales:

Jedes Dreieck ∆ABC, dessen Grundseite AB dem Durchmesser eines Halbkreises entspricht und dessen Ecke C auf dem Kreisbogen liegt,
ist rechtwinklig. Den Halbkreis mit dem eingeschlossenen Dreieck bezeichnet man kurz als „Thales-Kreis“.





  Aufgabe   Stift.gif

Arbeitsauftrag:

  • Konstruiere in dein Übungsheft einen Thales-Kreis.
  • Schreibe die besonderen Eigenschaften eines Thales-Kreis in dein Heft.
  • Füge sonstige Besonderheiten hinzu, die dir während des Bearbeitens des Lernpfades aufgefallen sind.



Team.gif
Entstanden unter Mitwirkung von:

Nico Stahl

Von „http://dmuw.zum.de/index.php?title=Lernpfade/Satz_des_Thales/Der_Satz_des_Thales&oldid=789“