Kongruenzabbildungen/Parallelverschiebung/Dreiecke und Winkel/Seite 4: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
Zeile 1: Zeile 1:
 
==Teilaufgabe d)==
 
==Teilaufgabe d)==
  
−
====<span style="color:#009ACD">Spieler<sub>5</sub></span> bleibt natürlich nicht stehen! Du kannst ihn mit Hilfe des Schiebereglers bewegen.====
+
'''In den vorherigen Teilaufgaben hast du einiges über Winkel und viele Eigenschaften von Dreiecken wiederholt.'''
  
−
<ggb_applet height="370" width="535" showResetIcon="true" filename="Fußballfeld_d).ggb" />
+
'''Jetzt wollen wir uns noch einmal etwas genauer mit den Winkeln beschäftigen, die du im Laufe deiner Schulzeit kennengelernt hast!'''
 +
 
 +
<ggb_applet height="290" width="480" showResetIcon="true" filename="FußballfeldMMe).ggb" />
 
<br>
 
<br>
−
<br>
+
<div class="zuordnungs-quiz">
−
====<span style="color:#009ACD">Spieler<sub>5</sub></span> kann sich so in Position bringen, dass die Drei spezielle Dreiecke bilden.====
+
<big>'''Ordne die Bilder, Winkel und Bezeichnungen den Oberbegriffen zu!'''</big><br>
−
 
+
Fällt es dir schwer, Zusammenhänge der Winkel im Applet zu erkennen, dann klicke auf das Kästchen "Parallelen zur Torauslinie anzeigen".
−
<quiz display="simple">
+
{|
−
{'''Kreuze an, welche Dreiecke entstehen können!'''}
+
| Wechselwinkel || Z-Winkel|| [[Bild:WwinkelMM.png]] || β und δ
−
 
+
|-
−
+ gleichseitiges Dreieck
+
| Stufenwinkel || F-Winkel|| [[Bild:SwinkelMM.png]] || γ und ε
−
 
+
|-
−
+ geichschenkliges Dreieck
+
| Ergänzungswinkel || [[Bild:EwinkelMM.png]] || E-Winkel || β und θ
−
 
+
|-
−
+ geichschenklig rechtwinkliges Dreieck
+
| Nebenwinkel|| [[Bild:NwinkelMM.png]]  || ε und μ
−
 
+
|}
−
- stumpfwinkliges Dreieck
+
−
 
+
−
+ spitzwinkliges Dreieck
+
−
 
+
−
</quiz>
+
−
 
+
−
'''2. Bearbeite jetzt den folgenden Lückentext! Ziehe die passenden Wörter in die Lücken und trage die richtigen Werte ein!'''
+
−
 
+
−
<div class="lueckentext-quiz">
+
−
 
+
−
Die drei bilden ein '''gleichseitiges''' Dreieck, wenn alle Seiten des Dreiecks eine Länge von '''8.5 (LE)''' haben. Die Winkel haben dann ein Maß von '''60 (°)'''. <br/>
+
−
Hat der Winkel β ein Maß von 90°, dann können die Fußballer auch ein '''gleichschenklig-rechtwinkliges''' Dreieck darstellen. Die beiden Schenkel b und c haben dann die Länge '''6 (LE)'''. <br/>
+
−
Die Winkel werden nie größer als '''90 (°)'''. Deshalb können nur '''spitzwinklige''' Dreiecke entstehen.
+
−
 
+
 
</div>
 
</div>
−
 
 
<br>
 
<br>
 
<br>
 
<br>
 +
===='''Jetzt fällt es dir bestimmt nicht mehr schwer, die fehlenden Winkel zu berechnen!'''====
 +
<div class="lueckentext-quiz">
  
−
'''3. Vielleicht ist dir schon aufgefallen, dass <span style="color:#009ACD">Spieler<sub>5</sub></span> auf einer ganz besonderen Geraden stürmt?'''<br/>
+
α = '''68 (°)'''<br />
−
'''Bearbeite dazu den folgenden Text, indem du die verdrehten Wörter entschlüsselst!'''
+
β = '''63 (°)'''<br />
−
<div class="schuettel-quiz">
+
γ = '''49 (°)'''<br />
−
 
+
θ = '''117 (°)'''<br />  
−
Diese Gerade enthält alle Punkte, die vom Spieler<sub>8</sub> und vom '''Torwart''' den '''gleichen''' '''Abstand''' haben. Sie halbiert die Strecke <span style="text-decoration: overline;">Spieler<sub>8</sub>Torwart</span> und steht '''senkrecht''' auf dieser.<br/>
+
λ = '''63 (°)'''<br />  
−
<span style="color:#009ACD">Spieler<sub>5</sub></span> bewegt sich also auf der '''Mittelsenkrechten''' zur Basis a des Dreiecks.
+
μ = '''131 (°)'''<br />
−
 
+
 
</div>
 
</div>
  
−
'''→[[Kongruenzabbildungen/Parallelverschiebung/Dreiecke_und_Winkel/Seite 5|Hier geht's zu Teilaufgabe e)]]'''
+
'''→[[Kongruenzabbildungen/Parallelverschiebung/Dreiecke_und_Winkel/Seite 5|Das war ganz schön viel. Zum Abschluss darfst du noch ein Memory lösen!]]'''

Version vom 15. Dezember 2009, 18:09 Uhr

Teilaufgabe d)

In den vorherigen Teilaufgaben hast du einiges über Winkel und viele Eigenschaften von Dreiecken wiederholt.

Jetzt wollen wir uns noch einmal etwas genauer mit den Winkeln beschäftigen, die du im Laufe deiner Schulzeit kennengelernt hast!


Ordne die Bilder, Winkel und Bezeichnungen den Oberbegriffen zu!
Fällt es dir schwer, Zusammenhänge der Winkel im Applet zu erkennen, dann klicke auf das Kästchen "Parallelen zur Torauslinie anzeigen".

Wechselwinkel Z-Winkel 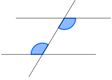WwinkelMM.png β und δ
Stufenwinkel F-Winkel SwinkelMM.png γ und ε
Ergänzungswinkel 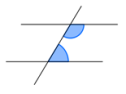EwinkelMM.png E-Winkel β und θ
Nebenwinkel 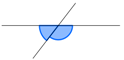NwinkelMM.png ε und μ



Jetzt fällt es dir bestimmt nicht mehr schwer, die fehlenden Winkel zu berechnen!

α = 68 (°)
β = 63 (°)
γ = 49 (°)
θ = 117 (°)
λ = 63 (°)
μ = 131 (°)

→Das war ganz schön viel. Zum Abschluss darfst du noch ein Memory lösen!

Von „http://dmuw.zum.de/index.php?title=Kongruenzabbildungen/Parallelverschiebung/Dreiecke_und_Winkel/Seite_4&oldid=9629“