Kongruenzabbildungen/Drehung/Seite 2: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
'''Wenn du am Schieberegler ziehst, kannst du das Flugzeug ein Looping fliegen lassen. ''' | '''Wenn du am Schieberegler ziehst, kannst du das Flugzeug ein Looping fliegen lassen. ''' | ||
| − | <ggb_applet height="545" width="535" showResetIcon="true" filename="Drehung_b)MM.ggb" /> | + | <div style="border: 2px solid #FFFFFF; background-color:#ffffff; padding:7px;"> |
| + | {|<br> | ||
| + | |<ggb_applet height="545" width="535" showResetIcon="true" filename="Drehung_b)MM.ggb" />|| | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 19: | Zeile 21: | ||
d) '''270(°)'''<br> | d) '''270(°)'''<br> | ||
| + | </div> | ||
| + | |} | ||
</div> | </div> | ||
Version vom 15. Dezember 2009, 20:48 Uhr
Teilaufgabe b)
Wenn du am Schieberegler ziehst, kannst du das Flugzeug ein Looping fliegen lassen.
|
Um wieviel Grad wurde das Flugzeug gedreht, wenn es a) 360(°), |
des Loopings,
des LoopingsSchauen wir uns die Drehung um 90° noch einmal ein bisschen genauer an!
Welche Koordinaten hat der Bildpunkt zu A(12|14) nach einer um den Punkt Z(1|1) mit dem Drehwinkel α = 90°?
A' (-12 (x-Koordinate) | 12 (y-Koordinate))
Berechne die Verbindungvektoren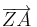 
(Urvektor) und 
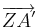(Bildvektor)!
Weißt du nicht mehr wie man Vektoren berechnet, dann lass dir folgenden Tipp anzeigen!
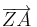(11 (x-Koordinate) | 13 (y-Koordinate))
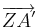(-13 (x-Koordinate) | 11 (y-Koordinate))
Das war doch gar nicht so schwer, oder? Üben wir das noch einmal an zwei Beispielen!
1. Gib zuerst die Koordinaten des Verbindungsvektor ZC an, wenn der Punkt C(2|14) um den Punkt Z(1|1) um 90° gedreht wird!
ZC (1 (x-Koordinate) | 13 (y-Koordinate))
Nach dem was du gerade gelernt hast ist es jetzt ganz einfach, die Koordinaten des Vektors ZC' zu berechnen!
ZC' (-12 (x-Koordinate) | 1 (y-Koordinate))
2. Das Flugzeug wird jetzt um das Zentrum Z(4|-2) um 90° gedreht. Berechne den Verbindungsvektor ZC' (C(2|14)).
ZC (1 (x-Koordinate) | 6 (y-Koordinate))
ZC' (-6 (x-Koordinate) | 1 (y-Koordinate))
Welche Koordinaten hat der Punkt C'?
C' (-3 (x-Koordinate) | 9 (y-Koordinate))
→Du hast das toll gemacht! Auf geht's zur nächsten Teilaufgabe!
