Kongruenzabbildungen/Drehung/Seite 2: Unterschied zwischen den Versionen
| Zeile 38: | Zeile 38: | ||
{{Versteckt| | {{Versteckt| | ||
Vektoren berechnet man nach der Vorschrift <span style="color:#EE2C2C">Spitze minus Fuß</span>.}}<br/> | Vektoren berechnet man nach der Vorschrift <span style="color:#EE2C2C">Spitze minus Fuß</span>.}}<br/> | ||
| − | <math>\overrightarrow { ZA }</math> | + | {| |
| − | <math>\overrightarrow { ZA' }</math> | + | |- |
| + | | <math>\overrightarrow { ZA }</math> = [[Bild:klammerMM.gif]] || | ||
| + | {| | ||
| + | |- | ||
| + | | '''11 (v<sub>x</sub>)''' | ||
| + | |- | ||
| + | | '''13 (v<sub>y</sub>)''' | ||
| + | |} | ||
| + | || [[Bild:klammer2MM.gif]] | ||
| + | |} | ||
| + | {| | ||
| + | |- | ||
| + | | <math>\overrightarrow { ZA' }</math> = [[Bild:klammerMM.gif]] || | ||
| + | {| | ||
| + | |- | ||
| + | | '''-13 (v<sub>x</sub>)''' | ||
| + | |- | ||
| + | | '''11 (v<sub>y</sub>)''' | ||
| + | |} | ||
| + | || [[Bild:klammer2MM.gif]] | ||
| + | |} | ||
</div> | </div> | ||
Version vom 16. Dezember 2009, 15:38 Uhr
Teilaufgabe b)
Wenn du am Schieberegler ziehst, kannst du das Flugzeug ein Looping fliegen lassen.
|
Um wieviel Grad wurde das Flugzeug gedreht, wenn es a) 360(°), |
Schauen wir uns die Drehung um 90° noch einmal ein bisschen genauer an!
Das war doch gar nicht so schwer, oder? Üben wir das noch einmal an zwei Beispielen!
1. Gib zuerst die Koordinaten des Verbindungsvektor ZC an, wenn der Punkt C(2|14) um den Punkt Z(1|1) um 90° gedreht wird!
ZC (1 (x-Koordinate) | 13 (y-Koordinate))
Nach dem was du gerade gelernt hast ist es jetzt ganz einfach, die Koordinaten des Vektors ZC' zu berechnen!
ZC' (-12 (x-Koordinate) | 1 (y-Koordinate))
2. Das Flugzeug wird jetzt um das Zentrum Z(4|-2) um 90° gedreht. Berechne den Verbindungsvektor ZC' (C(2|14)).
ZC (1 (x-Koordinate) | 6 (y-Koordinate))
ZC' (-6 (x-Koordinate) | 1 (y-Koordinate))
Welche Koordinaten hat der Punkt C'?
C' (-3 (x-Koordinate) | 9 (y-Koordinate))
→Du hast das toll gemacht! Auf geht's zur nächsten Teilaufgabe!
 des Loopings,
des Loopings, des Loopings
des Loopings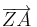 (Urvektor) und
(Urvektor) und 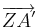 (Bildvektor)!
(Bildvektor)!
