Seite 2

Teilaufgabe b)

Der Bus muss immer wieder eine Pause machen.

Er hält das erste Mal nach 12,2m Fahrt an. Trage die Koordinaten der hinteren Stoßstange (A‘) und die der vorderen Stoßstange (B') ein. Die Urpunkte haben die Koordinaten A(2|2) und B(8|3). A' (14 (x-Koordinate) | 4 (y-Koordinate)), B' (20 (x-Koordinate) | 5 (y-Koordinate)) Um welchen Vektor wurde der Bus verschoben? Wenn du nicht mehr genau weißt, wie man Vektoren berechnet, verwende den Tipp unter dem Kasten! $\vec v$ = 12 (x-Koordinate des Vektors) 2 (y-Koordinate des Vektors) Tipp anzeigen verstecken Vektoren berechnet man nach der Merkregel Spitze minus Fuß! Überlege dir, welche Punkte Anfangs- und Endpunkte des Vektors sind!

Der Bus macht die nächste Pause nach insgesamt 15,2m Fahrt. Welche Koordinaten haben die vordere und hintere Stoßstange jetzt?
A' (17 (x-Koordinate) | 4,5 (y-Koordinate)),
B' (23 (x-Koordinate) | 5,5 (y-Koordinate))

Um welchen Vektor wurde der Bus verschoben?

$\vec v$ =

15 (x-Koordinate des Vektors) 2,5 (y-Koordinate des Vektors)

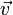Der vordere Eckpunkt des Daches hat die Koordinaten E(6|6). Er wurde um den Vektor 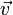$\vec v$ = $\ {18 \choose 3}$ verschoben. Welche Koordinaten hat der Bildpunkt E'?
E' (24 (x-Koordinate) | 9 (y-Koordinate))

Wie viele Meter ist der Bus bis zu diesem Punkt gefahren?
18,2 (m)

 

 

Teilaufgabe c)

Jetzt wird es schon etwas schwerer. Du kannst das Applet nämlich nicht mehr zur Hilfe nehmen. Aber du schaffst das bestimmt!

Beim nächsten Zwischenstop des Busses hat der vordere Eckpunkt des Daches E(6|6) die Koodinaten E(30|10).
Um welchen Vektor wurde der Bus also verschoben?

$\vec v$ =

24 (x-Koordinate des Vektors) 4 (y-Koordinate des Vektors)

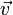Der Bus hat sein Ziel erreicht, wenn er um den Vektor 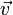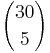$\vec v$ = $\ {30 \choose 5}$ verschoben wurde.
Welche Koordinaten haben dann die Bilder der hinteren Stoßstange A(2|2) und der vorderen Stoßstange B(8|3)?
A' (32 (x-Koordinate) | 7 (y-Koordinate)),
B' (38 (x-Koordinate) | 8 (y-Koordinate)),

Das war ganz schön viel zu rechnen. Aber du hast das ganz toll gemacht!

→Auf geht's zur nächsten Teilaufgabe!