| richtig | falsch
| |
| | u : d = 3,14 |
| → | Der Umfang steht zum Durchmesser im Verhältnis 3,14. |
| | 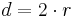 |
| → | Der Durchmesser ist doppelt so groß wie der Radius eines Kreises. |
| | 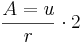 |
| → | 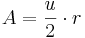 . . |
| | 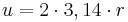 |
| → | Der Umfang ist doppelt so groß wie die Kreiszahl mal den Radius. |
| | 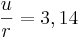 |
| → | Der Umfang steht zum Durchmesser im Verhältnis 3,14. |
| | 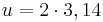 |
| → | Der Umfang ist immer auch abhängig vom Radius. |
| | 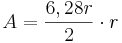 |
| → | Kürze mit 2 und du erhälst die bekannte Formel zur Flächenberechnung am Kreis. |
| | 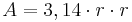 |
| → | Die Formel zur Berechnung des Flächeninhaltes lautet 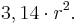 |
| | 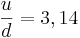 |
| → | Die Formel zur Berechnung des Flächeninhaltes lautet 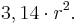 |
| | 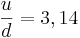 |
| → | Der Umfang steht zum Durchmesser im Verhältnis 3,14. |
| | 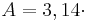 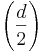  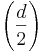 |
| → | Die Formel zur Berechnung des Flächeninhaltes lautet 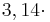  und und 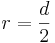 . . |