2.Station

1. Station: Ähnlichkeitsabbildung - Exkurs: Weitere Beispiele einer zentrischen Streckung - 2. Station: Streckungsfaktor - 3. Station: Berechnung der Streckenlängen und des Streckungsfaktors - 4. Station: Zusammenfassung - 5. Station: Übungen - 6. Station: Wissenswertes

2. Station: Streckungsfaktor

In dem nächsten Fall ist das Urbild ein Dreieck, dass du zentrisch strecken kannst, indem du an dem Schieberegler ziehst.

Der Schieberegler durchläuft die positiven Zahlen von k=0 bis k=3.

Was verändert sich? Orientiere dich dabei an diesen Fragen: 1. Auf welcher Seite von Z liegen das Urbild und das Bild? auf derselben Seite auf verschiedenen Seiten 2. Was liegt bei k>1 vor? eine Vergrößerung eine Verkleinerung die Identität 3. Was liegt bei 0<k<1 vor? eine Vergrößerung eine Verkleinerung die Identität 4. Was liegt bei k=1 vor? eine Vergrößerung eine Verkleinerung die Identität 5. Was passiert wenn k=0 ist? es erfolgt keine zentrische Streckung es erfolgt eine zentrische Streckung Punkte: 0 / 0

Was sind die Unterschiede, wenn du dieses Dreieck zentrisch streckst? Dieses mal durchläuft der

Schieberegler die negativen Zahlen von k=-3 bis k=0.

Was verändert sich? Orientiere dich dabei an diesen Fragen: 1. Auf welcher Seite von Z liegen das Urbild und das Bild? auf derselben Seite auf verschiedenen Seiten 2. Was liegt bei k< -1 vor? eine Vergrößerung eine Verkleinerung die Identität eine Spiegelung 3. Was liegt bei 0>k> -1 vor? eine Vergrößerung eine Verkleinerung die Identität eine Spiegelun) 4. Was liegt bei k= -1 vor? eine Vergrößerung eine Verkleinerung die Identität eine Spiegelung Punkte: 0 / 0

Um herauszufinden was das k bedeutet, musst du dir jetzt bei dieser zentrischen Streckung anschauen, wie

sich die Streckenlängen verändern, wenn du k veränderst. Dazu musst du dir die Streckenlängen anzeigen lassen.

Was verändert sich? Orientiere dich dabei an diesen Fragen: 1. Wie verändert sich die Streckenlänge ZB? Sie bleibt immer gleich. Sie ist variabel. 2. Wie verändert sich die Streckenlänge ZB'? Sie bleibt immer gleich. Sie ist variabel. 3. Wie verhält sich k? Es bleibt immer gleich. Es ist variabel. Punkte: 0 / 0

Die Werte, die sich aus der Änderung von k ergeben, wurden in zwei Tabellen zusammengefasst.

In der linken sind die Werte für k von 2 bis 0, in der rechten für k von -2 bis 0.

Arbeitsauftrag:

1. Betrachte zunächst nur die linke Tabelle und stelle eine Vermutung auf, wie sich die Länge von ZB' ändert im Vergleich zur Länge von ZB?

(Tipp: Betrachte auch den Wert von k!)

2. Vergleiche die Zeilen mit der selben Hintergrundfarbe! Was haben sie gemeinsam? Was sind die Unterschiede?

k ZB ZB' 2 4 8 1.5 4 6 1 4 4 0.5 4 2 0 4 0

k ZB ZB' -2 4 8 -1.5 4 6 -1 4 4 -0.5 4 2 0 4 0

Hier kannst du deine Vermutung mit der von Dia vergleichen:

[Anzeigen][Verstecken]

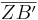1. $\overline{ZB'}$ ist k-mal so lang wie $\overline{ZB}$.

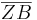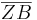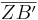2. Die Längen der Strecken $\overline{ZB}$ und $\overline{ZB'}$ bleiben gleich, wenn sich das Vorzeichen von k ändert.

Dia ist nach ihren Vermutungen total verwirrt. Sie versteht nicht warum der Wert von ZB' gleich bleibt, wenn sich das Vorzeichen von k ändert.

Vielleicht kannst du ihr helfen, indem du ihre Fragen beantwortest:

1. Kann eine Streckenlänge ein negatives Vorzeichen haben?

	nein
	ja

2. Wie kann man eine negative Zahl in eine positive Zahl umwandeln, sodass der Wert gleich bleibt, sich jedoch aber eine positive Zahl nicht in eine negative Zahl umwandelt?

	durch Quadrieren
	mit Hilfe von Betragsstrichen
	durch Multiplikation mit -1

Punkte: 0 / 0

Prima! Dank dir versteht jetzt Dia, wie die Werte für ZB' entstehen.

Mit deiner Hilfe und ihrer Vermutungen kann sie eine allgemeingültige Aussage machen.

Teste durch Einsetzen der richtigen Wörter, ob auch du dahinter gekommen bist:

Die Länge von ZB ist |k|-mal so lang wie die Länge von ZB'.

Hier siehst du was das k bedeutet. Merke es dir, denn später wirst du darüber abgefragt!

k bezeichnet man als den Streckungsfaktor. Er gibt den Maßstab an, in dem das Bild vergrößert wurde.

Weiter zur 3. Station: Berechnung der Streckenlängen und des Streckungsfaktors

Zurück zum Exkurs: Weitere Beispiele einer zentrischen Streckung