Die Normalparabel stellt sich vor
|
Lernpfad
|
Auf gehts:
Eine neue Klasse von Funktionen stellt sich vor!
Hast du schon mal was von der Parabel gehört?
Vielleicht kennst du ja schon die Parabel, falls nicht, versuche durch Zuordnung die Normalparabel zu entdecken.
Tipps:
- Zwei der drei dargestellten Grafiken müssten dir bekannt sein!
- Ziehe die vorgegebenen Lösungen zur richtigen Grafik durch festhalten der linken Maustaste
| Datei:Normalparabel.jpg | Normalparabel |
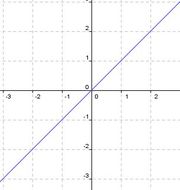 |
Lineare Funktion |
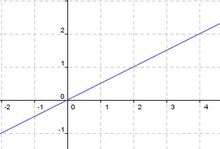 |
f(x)= 0,5x |
Super! Nun weißt du wie die Parabel aussieht, wenn du es nicht schon längst gewusst hast.
Wie du dir sicher denken kannst, kann man die Normalparabel auch als Funktion darstellen.
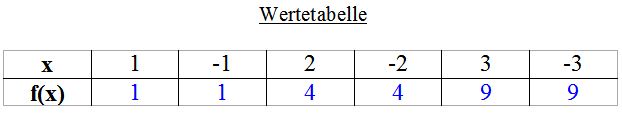
Dafür wollen wir eine Wertetabelle erstellen.
Aufgabe:
In der aufgeführten Normalparabel kannst du die Punkte zum erstellen einer Wertetabelle erkennen.
a) Nehme ein Blatt Papier und suche für die folgenden x-Werte die zugehörigen y-Werte und stelle eine Wertetabelle auf für:
- x1 = 1
- x2 = -1
- x3 = 2
- x4 = -2
- x5 = 3
- x6 = -3
b) Was fällt dir beim y-Wert im Bezug zum x-Wert auf?
Hilfe:
Eine Aussage stimmt!
- Der y-Wert ist immer das doppelte des x-Wertes: f(x)
 2x
2x
- Der x-Wert und der y-Wert stehen in keinem Zusammenhang
- Der y-Wert entsteht aus dem Quadrat des x-Wertes: f(x)
 x2
x2
Lösung:
 x2
x2
30px Merke
Die Normalparabel besitzt die Funktionsgleichung der Form: f(x) Da sich jeder y-Wert aus dem Quadrat des x-Wertes ergibt, nennt man die Normalparabel auch quadratische Funktion. |
Als nächstes wollen wir die Eigenschaften der Normalparabel erarbeiten.
Bearbeite das folgende "Prettytable":
Normalparabel f(x) x2 x2 |
Aufgabenstellung und Lückentext: |
|---|---|
| Aufgabenstellung: *Betrachte die folgende Grafik und versuche den Lückentext mit den vorgegebenen Hilfen zu lösen. Ziehe dafür die möglichen Lösungen mit gehaltener linker Maustaste in die Felder.
Anders als bei den linearen Funktionen ist die Steigung der Normalparabel nicht konstant. Es lässt sich feststellen, dass die Normalparabel symmetrisch zur y-Achse und nach oben geöffnet ist. Daraus lässt sich folgern, dass alle Funktionswerte größer oder gleich 0 sind. Die Normalparabel besitzt zudem einen tiefsten Punkt im Koordinatenursprung bei Punkt S |
Prima! Damit kennst du nun die wichtigsten Eigenschaften der Normalparabel.
Wir wollen Sie noch mal zusammenfassen!!
30px Merke
Die Normalparabel: * Ist eine Parabel mit der Funktionsgleichung f(x) |
KNIFFELAUFGABE:
Du kennst zwar nun schon die Eigenschaften der Normalparabel, aber eine er Eigenschaften soll nun noch mal genauer herausgehoben werden. Dazu musst du eine kleine Kniffelaufgabe lösen. Keine Angst, sie ist nicht zu schwer.
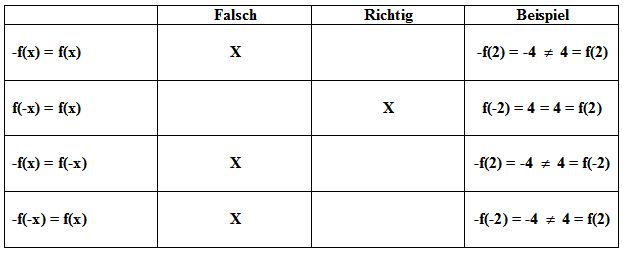
Nehme einen Stift und ein Blatt zur Hand und überprüfe welche der folgenden Aussagen richtig oder falsch ist und gebe ein Beispiel für den x-Wert 2 an. Was stellst du fest?
Betrachtet werden soll natürlich die quadratische Funktion f(x) x2
x2
Tipp!!
Es geht um die Symmetrieeigenschaft der Normalparabel.
Hilfe: Falls du Probleme hast ein Beispiel aufzustellen, findest du hier eine Hilfestellung:
- -f(x)
 -f(-2)
-f(-2) -(-x)2
-(-x)2 -(-2)2
-(-2)2 -4 ist ungleich zu f(x)
-4 ist ungleich zu f(x) f(2)
f(2) (x)2
(x)2 22
22 4
4
Lösung:
Wie du hoffentlich herausgefunden hast, ist das einzig richtige Ergebnis: f(-x) f(x)
Warum ist das so?
Aufgrund der Symmetrieeigenschaft der Normalparabel wird jedem x-Wert egal ob positiv oder negativ, der gleiche y-Wert zugeordnet.
f(x)
Warum ist das so?
Aufgrund der Symmetrieeigenschaft der Normalparabel wird jedem x-Wert egal ob positiv oder negativ, der gleiche y-Wert zugeordnet.
30px Merke
Aufgrund der Symmetrieeigenschaften der Normalparabel gilt: f(-x) |
Hier ist nun die Einführung der Normalparabel als die einfachste Form der quadratischen Funktion abgeschlossen.
In den folgenden Lerneinheiten wird nun mit dieser Parabel gearbeitet. Neue Parameter werden die Normalparabel verändern, aber siehe selbst!!

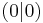 . Dieser Punkt wird als Scheitelpunkt S oder kurz Scheitel bezeichnet.
. Dieser Punkt wird als Scheitelpunkt S oder kurz Scheitel bezeichnet.
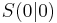 liegt.
liegt.