5.Station
Aus DMUW-Wiki
< Lernpfade | Zentrische Streckung | Vierstreckensatz
Version vom 12. Juli 2009, 10:37 Uhr von Leonie Porzelt (Diskussion | Beiträge)
1. Station: Erster Vierstreckensatz - Schenkellösung - 2. Station: Erster Vierstreckensatz - Abschnittlösung - 3. Station: Zweiter Vierstreckensatz - 4. Station: Zusammenfassung - 5. Station: Übung
5. Station: Übung
1. Aufgabe
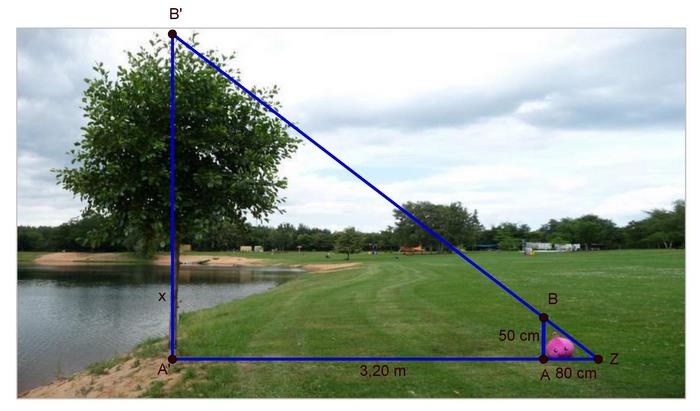
Berechne die Höhe des Baumes in deinem Heft. Entnimm die Werte aus dem Bild.
2. Aufgabe
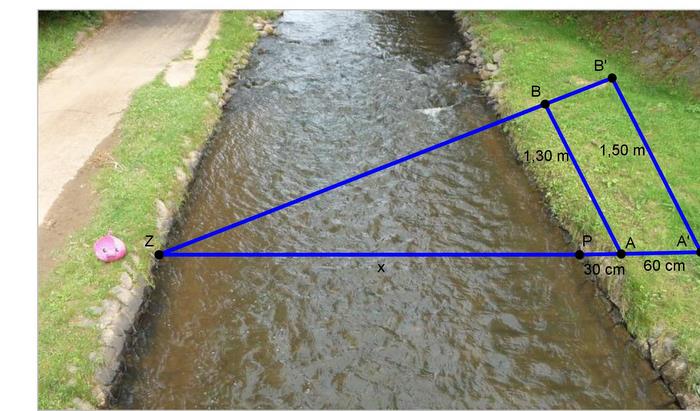
- Hilf Panto herauszufinden, wie breit der Fluss ist, indem du mit den im Bild angegebenen Maßen die gesuchte Entfernung ZP berechnest.
3. Aufgabe
- Zwei Parfümflaschen werden so miteinander verbunden, dass das obere Ende der einen mit dem unteren Ende der anderen Parfümflasche
- verbunden ist.
- a) Wie hoch befindet sich der Kreuzungspunkt der Seile über dem Erdboden, wenn die erste Parfümflasche eine Höhe von
- 12 cm und und die zweite eine Höhe von 18 cm hat?
- b) Warum wurde der Abstand der zwei Parfümflaschen nicht angegeben? (Tipp: Bewege im Applet die große Parfümflasche und beobachte
- was passiert!)
| Berechne die Aufgabe in deinem Heft und trage hier deine Lösung (gerundet auf eine Nachkommastelle) mit Angabe der Einheit (cm) ein!
x = 7,2 cm (Tipp: Leerzeichen zwischen Zahl und Einheit nicht vergessen!). Falls du alleine nicht weiter kommst, lass dir den 1. Tipp anzeigen!
Da sich die Höhe h nicht ändert, wenn der Abstand geändert wird, kannst du für
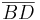 einen beliebigen Wert einsetzen. einen beliebigen Wert einsetzen.Falls dir der 1. Tipp auch nich weiterhilft, hier noch ein 2. Tipp:
Lass dich nicht durch den Punkt Z verwirren. Betrachte einmal den Punkt A und ein weiteres mal den Punkt B als Streckungszentrum. Für die Strecke
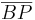 oder die Strecke oder die Strecke 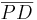 musst du eine weitere Variable einsetzen (z.B. musst du eine weitere Variable einsetzen (z.B. 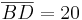  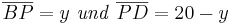 . . |
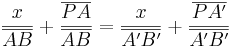
 Zurück zur 4. Station: Zusammenfassung
Zurück zur 4. Station: Zusammenfassung
