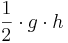Flächeninhalt ebener Figuren- Teil 2

Flächeninhalt Dreieck

---

Einstieg

---

Vorüberlegungen: Dem Dreieck auf der Spur

1. Teil: Wie ändert sich der Flächeninhalt?

Aufgabenstellung:

• Ziehe beliebig am Eckpunkt C des Dreiecks ABC. Beobachte, wie sich der Flächeninhalt verändert.
• Zeige für die Fragen die vier Geraden an und variiere wieder den Eckpunkt C.
  

1. Wann wird der Flächeninhalt größer? je weiter weg man C von der Geraden AB bewegt. je weiter weg man C zur Geraden AB bewegt. 2. Auf welcher Geraden musst Du C bewegen, damit der Flächeninhalt gleich bleibt? C wird auf der Senkrechten zur Geraden AB bewegt C wird auf der Parallelen zur Geraden AB bewegt C wird auf der grünen Geraden bewegt Punkte: 0 / 0 kein Punkt: Schaue Dir die Animation genauer an 1 Punkt: Das hast Du schon gut gelöst! 2 Punkte:Das hast Du sehr gut gemacht! Du kannst jetzt mit dem nächsten Abschnitt fortfahren!

2. Teil: Wir vermuten weiter

1. Ziehe an den Eckpunkten A und B, beobachte, wie sich die Länge der Grundseite verändert.
2. Beobachte während Du die Länge der Grundseite veränderst, wie sich der Flächeninhalt verhält

Aufgabenstellung: (Die Längen sind im Applet in Zentimetern angegeben) 1.Vergrößere die Grundseite, was passiert mit dem Flächeninhalt? +Der Flächeninhalt wird größer. -Der Flächeninhalt wird kleiner. -Der Flächeninhalt ändert sich nicht. 2.. Du kannst die Höhe verändern, indem Du am Schieberegler ziehst. Beobachte was mit dem Flächeninhalt passiert. Verkleinere die Höhe, was passiert mit dem Flächeninhalt? -Der Flächeninhalt wird größer. +Der Flächeninhalt wird kleiner. -Der Flächeninhalt ändert sich nicht. 3. Stelle die Höhe auf 4cm ein und die Länge der Grundseite auf 2cm. Wo liegt die Höhe? Wie groß ist der Flächeninhalt? 4. Wie lang muss die Höhe sein, wenn der Flächeninhalt cm² und die Grundseite cm ist?

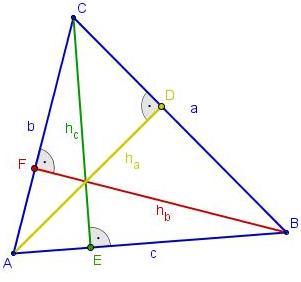
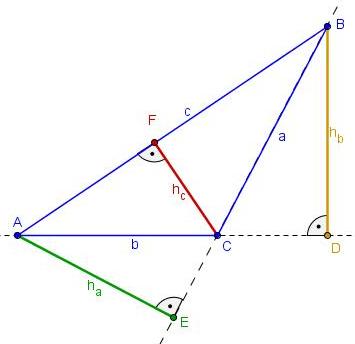
Höhen im Dreieck

Auch hier darfst Du wieder konstruieren.

Öffne wieder die Geogebra Datei durch Klick auf den Button. Konstruiere eine Höhe im dem vorgegebenen Dreieck, nach folgender Aufgabenstellung:

1. Zeichne vom Punkt C aus eine senkrechte Gerade zur gegenüberliegenden Seite c des Dreiecks.
2. Schneide wieder diese Gerade mit der Seite c.
3. Blende die Gerade aus!
4. Konstruiere eine Strecke zwischen dem erhaltenen Schnittpunkt und der Ecke C.
   

Sehr schön! Was Du konstruiert hast ist eine Höhe des Dreiecks vom Eckpunkt C aus, auf die gegenüberliegende Seite.

5. Bewege den Eckpunkt C nach Links und Rechts. Was passiert mit der Höhe?

[Lösung anzeigen][Lösung ausblenden]

Bewegt man den Eckpunkt C so weit, dass ein Basiswinkel (nicht der Winkel am Eckpunkt C) größer als 90° wird, so liegt die Höhe außerhalb des Dreiecks! Dies ist in stumpfwinkligen Dreiecken der Fall!

So löst man das Problem:

1. Konstruiere eine Gerade durch A und B
2. Zeichne eine Senkrechte vom Punkt C zu dieser Geraden!
3. Schneide diese Senkrechte Gerade mit der Geraden durch AB. Blende die Senkrechte Gerade wieder aus.
4. Verbinde den erhaltenen Schnittpunkt mit C

Was Du nun konstruiert hast, ist wieder eine Höhe vom Eckpunkt C aus. Doch diese kann auch außerhalb liegen!! Teste dies durch Bewegen von C!!

Zusammenfassung

Auch die Eigenschaften der Höhen im Dreieck solltest du wissen. Daher wurden sie hier zusammengefasst. Wenn Du möchtest, kannst Du den Merkkasten in Dein Heft übrtragen.

Die Höhe im Dreieck ist der Abstand von einem Eckpunkt des Dreiecks zur gegenüberliegenden Seite. Die Punkte D,E,F nennt man Höhenfußpunkte Beispiel: Hier siehst Du eine Tabelle mit den Bezeichnungen für das Dreieck aus dem obigen Bild. Füge die passenden Bezeichnungen in der Tabelle ein Grundlinien Länge der Grundlinien Höhen zu den Grundlinien Länge der Höhen [AB] c [CE] hc [BC] a [AD] ha [AC] b [BF] hb In der Konstruktionsaufgabe hast Du einen Spezialfall Kennen gelernt: Im stumpfwinkligen Dreieck liegen zwei Höhen außerhalb des Dreiecks. Die Höhe ist hier der Abstand vom Eckpunkt zur Geraden durch die beiden anderen Eckpunkte des Dreiecks. Die Höhen im Dreieck schneiden sich in einem Punkt, dem Höhenschnittpunkt.

Die Flächeninhaltsformel des Dreiecks

Mathematik scheint manchmal wie Zauberei...Warum?? Das erfährst Du im nächsten Abschnitt.

Fast wie Zauberei! Zweimal Unbekannt = Bekannt?

Wir wollen die Flächeninhaltsformel für Dreiecke herausfinden.

Doch, wie könnte man das nur machen?

In diesem Applet siehst Du das Dreieck ABC. Bearbeite die nebenstehende Aufgabenstellung.

Aufgabenstellung: Ziehe am Schieberegler und beobachte, was passiert. Hilft uns dieses Modell weiter, die Formel für das Dreieck zu finden? Das Dreieck wird durch ein zweites kongruentes Dreieck zum Parallelogramm (Figur eintragen) ergänzt. Warum ist dieses zweite Dreieck kongruent zum ersten? Das Dreieck geht durch Drehung um den Mittelpunkt aus dem ersten Dreieck hervor. Dies ist eine Kongruenz-abbildung. Berechne den Flächeninhalt des Parallelogramms Der Flächeninhalt des Parallelogramms beträgt 12 (cm²) Wie groß ist der Flächeninhalt eines Dreiecks? Der Flächeninhalt eines Dreiecks beträgt 6 (cm²)

Übungsaufgaben

Leite die allgemeine Flächeninhaltsformel für Dreiecke her!

Bedenke nochmals, welche Flächeninhaltsformel Du vor Kurzem erst Kennen gelernt hast

Aufgabenstellung: Ergänze die fehlenden Felder in der Rechnung.

Gesucht: F_Dreieck = ??

F_{Parallelogramm} = g $\cdot$ h
F_{Parallelogramm} = F_Dreieck + F_Dreieck
F_{Parallelogramm} = 2 $\cdot$ F_Dreieck
g $\cdot$ h = 2 $\cdot$ F_Dreieck
${1 \over 2}$ $\cdot$ g $\cdot$ h = F_Dreieck

Super! Du hast die Flächeninhaltsformel für Dreiecke gefunden.

• Begründe mit einem Prinzip, dass Du im ersten Lernpfad kennen gelernt hast, warum man die Formel auf diesem Wege herleiten kann. Gehe hier vom Flächeninhalt des Parallelogramms aus.
  
• Fülle den folgenden Lückentext aus.

Zerlegungsgleichheit ist das Stichwort! Die Flächeninhaltsformel für Dreiecke lässt sich herleiten, indem man ein Parallelogramm geeignet halbiert. Man halbiert dies entlang seiner Diagonalen.
Diese Halbierung zerlegt das Parallelogramm in zwei kongruente Dreiecke, die jeweils den gleichen Flächeninhalt besitzen und deren Gesamtflächeninhalt dem des Parallelogramms entspricht. Ein Dreieck ist damit halb so groß wie ein Parallelogramm mit derselben Grundseite und Höhe .

---

---

Zusammenfassung

Übertrage den roten Merkkasten in dein Heft, damit Du die Flächeninhaltsformel für Dreiecke auch Zuhause nachschauen kannst:

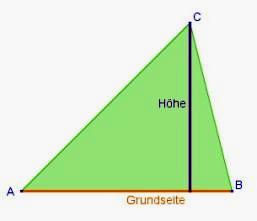
Den Flächeninhalt des Dreiecks berechnet man durch FDreieck = ${1 \over 2} \cdot g \cdot h$ mit g als Grundseite und h als der dazugehörigen Höhe.

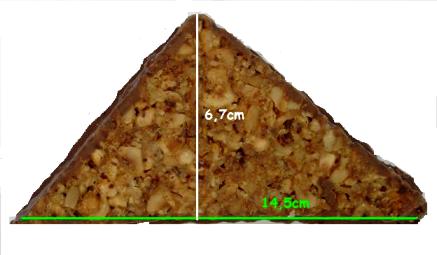
Aufgabe 2: Nussecke backen

Maja hat 30 Nussecken gebacken und möchte deren Oberseite vollständig mit Schokolade überziehen. Das Bild zeigt eine Nussecke, die 6,7 cm hoch und 14,5 cm breit ist. Alle Nussecken sind gleich groß.

Frage: Für welche Fläche braucht Maja Schokolade?

Sie benötigt für eine Fläche von 1457,25 ( nur die Zahl eintragen!) cm² Schokolade

---

Vertiefen und Erweitern

Du hast nun eine Möglichkeit kennen gelernt, wie man die Flächeninhaltsformel für Dreiecke herleiten kann.

Dies ist aber natürlich nicht der einzige Lösungsansatz.

Im nächsten Abschnitt lernst Du weitere kennen.

Versuche die Lösungsideen nachzuvollziehen und bearbeite die Aufgabenstellungen. Leite daraus jeweils algebraisch die Flächeninhaltsformel für Dreiecke her.

Herleitungsidee 2

---

Aufgabenstellung: 1.Wie wurde das Dreieck zerlegt? [Lösung anzeigen][Lösung ausblenden] Man zeichnet die Mittelparallele des Dreiecks zur Grundseite ein und schneidet diese mit der Höhe zu dieser Grundseite. 2.Welche Figur ensteht? [Lösung anzeigen][Lösung ausblenden] Es entsteht ein Rechteck 3.Wie erhält man die Figur? [Lösung anzeigen][Lösung ausblenden] Durch Zerlegung des Ursprungsdreiecks und Ergänzung 5.Um welche Punkte werden die Teildreiecke gedreht? Um wieviel Grad werden sie gedreht?[Lösung anzeigen][Lösung ausblenden] Die Teildreiecke werden um die Seitenmittelpunkte gedreht. Sie werden um 180° gedreht. Es handelt sich also um eine Kongruenzabbildung. 6.Welche Höhe besitzt die neue Figur, im Vergleich zum Ursprungsdreieck?[Lösung anzeigen][Lösung ausblenden] Die Höhe des Rechtecks ist halb so groß, wie die Höhe des Ausgangsdreiecks 7.Welche Länge besitzt ihre Grundseite?[Lösung anzeigen][Lösung ausblenden] Die Grundseite ist genauso lang, wie die des Ausgangsdreiecks.

Wie kann man für diese Methode die Flächeninhaltsformel des Dreiecks berechnen??

F_Rechteck = g $\cdot$ h₂

Aufgrund der Zerlegungsgleichheit gilt:

F_Rechteck = F_Dreieck

Für die Höhen gilt:

h₂ = ${1 \over 2}$ $\cdot$ h₁

Einsetzen in Formel für Rechteck:

F_Dreieck = ${1 \over 2}$ g $\cdot$ h₁

---

Herleitungsidee 3

---

Aufgabenstellung: 1. Wie wurde das Dreieck zerlegt? [Lösung anzeigen][Lösung ausblenden] Es wurde die zur Grundseite parallele Strecke zwischen den Seitenmittelpunkten eingezeichnet. 2.Welche Figur ensteht bei der Ergänzung? [Lösung anzeigen][Lösung ausblenden] Es ensteht ein Paralellogramm 3.Wie entsteht diese Figur? [Lösung anzeigen][Lösung ausblenden] Das Parallelogramm ensteht durch Zerlegung des großen Dreiecks in ein kleines Teildreieck und ein Trapez. Durch Drehen des kleinen Teildreiecks ergänzt man das Trapez zum Parallelogramm 4. Um welchen Punkt wird das kleine Teildreieck gedreht? Um wieviel Grad wird es gedreht? [Lösung anzeigen][Lösung ausblenden] Das kleine Teildreieck wird um 180 ° um einen Seitenmittelpunkt gedreht. Damit ist klar, dass es sich um eine Kongruenzabbildung handelt. 5. Welche Höhe besitzt die neue Figur im Vergleich zum Dreieck [Lösung anzeigen][Lösung ausblenden] Die Höhe des Parallelogramms ist halb so groß, wie die des Ausgangsdreiecks. Das Paralellogramm besitzt aber die gleiche Länge der Grundseite

Wie kann man für diese Methode die Flächeninhaltsformel des Dreiecks berechnen??

F_{Parallelogramm} = g $\cdot$ h₂

Aufgrund der Zerlegungsgleichheit gilt:

F_{Parallelogrammk} = F_Dreieck

Für die Höhen gilt:

h₂ = ${1 \over 2}$ $\cdot$ h

Einsetzen in Formel für Parallelogramm:

F_Dreieck = ${1 \over 2}$ g $\cdot$ h

Wie Du siehst, ähneln sich diese beiden Herleitungsideen:
In der ersten Variante zerlegt man das Dreieck geeignet und ergänzt zum Rechteck mit gleicher Grundseite und halber Höhe...
und in der zweiten Variante zerlegt man das Dreieck und ergänzt zu einem Parallelogramm mit gleicher Länge der Grundseite und halber Höhe.

---

Herleitungsidee 4

---

Wir haben für die Hilfsfigur, deren Flächeninhalt man kennt das Ausgangsdreieck so zerlegt, dass die Höhe halbiert und die Länge der Grundseite gleich beibehalten wird.

Wie Du ahnst gibt es noch eine weitere Möglichkeit:

Aufgabenstellung: 1.Welche Figur ensteht bei der Ergänzung? [Lösung anzeigen][Lösung ausblenden] Es entsteht ein Rechteck 2. Um welchen Punkt werden jeweils die Teildreiecke gedreht? Um wieviel Grad werden sie gedreht? [Lösung anzeigen][Lösung ausblenden] Die Teildreiecke werden jeweils um die Seitenmittelpunkte gedreht, dabei dreht man um 180°. Dies ist eine Kongruenzabbildung 3.Welche Höhe besitzt die erhaltene Figur? [Lösung anzeigen][Lösung ausblenden] Die Höhe des Rechtecks entspricht der Höhe des Ausgangsdreiecks 4.Zeige, dass die Grundseite g der neuen Figur halb so lang ist, wie die Grundseite des Dreiecks! Tipp: Ergänze zum Rechteck und beobachte dabei die Teilstrecken s und t gDreieck = s + s + t + t gDreieck = 2 $\cdot$ s + 2$\cdot$ t = 2 $\cdot$(s + t) gRechteck= s + t => gRechteck = ${1 \over 2}$ $\cdot$ gDreieck

Wie kann man daraus die Flächeninhaltsformel für das Dreieck berechnen?

F_Rechteck = g_Rechteck $\cdot$ h

Aufgrund der Zerlegungsgleichheit gilt:

F_Rechteck = F_Dreieck

Für die Grundseiten gilt:

g_Rechteck = ${1 \over 2}$ $\cdot$ g_Dreieck

Einsetzen in Formel für Rechteck:

F_Dreieck = ${1 \over 2}$ g_Dreieck $\cdot$ h

---