Vertiefen und Erweitern zum Parallelogramm
Du hast alle Aufgaben gelöst? Sehr gut! Für die ganz Schnellen gibt es hier ein paar weitere Herleitungsideen.
Variante zur Herleitung
Eine weitere Lösungsidee ist in der nächsten Darstellung verborgen:
Aufgabenstellung:
In diesem Fall werden nicht die Parallelogrammseiten betrachtet, die auf den Parallelen Geraden liegen, sondern das andere Seitenpaar. Entsprechend wird die dazugehörige Höhe zur Flächenberechnung gewählt! |
 |
Zur Berechnung der Flächeninhaltsformel kann jede Seite des Parallelogrammes als Grundseite und die zugehörige Höhe genommen werden. |
Flächeninhaltsgleiche Parallelogramme
Erinnerst Du Dich noch??
Du hast bereits im ersten Lernpfad mit dem Prinzip der Ergänzungsgleichheit nachgewiesen, dass das Parallelogramm und das Quadrat den gleichen Flächeninhalt besitzen. Wie kann man das ohne Ergänzungsgleichheit zeigen???
| Erkläre, warum das blaue Parallelogramme den gleichen Flächeninhalt wie das rote Rechteck besitzt. Berechne zunächst den Flächeninhalt des Rechtecks. Tipp: Du kannst auch die Höhe anzeigen lassen.
Der Flächeninhalt des Rechtecks beträgt: 12 (cm²) | |
|
Du kannst das Parallelogramm mit dem Schieberegler ziehen: | |
| Fülle den nachfolgenden Lückentext aus:
Das Parallelogramm hat den gleichen Flächeninhalt wie das rote Rechteck, da beide dieselbe Grundseite besitzen. Auch die Höhe ist bei beiden gleich, das die verschiebbaren Seite auf der gleichen Parallele zur Grundseite liegt und somit den gleichen Abstand zur Grundseite besitzt.
|
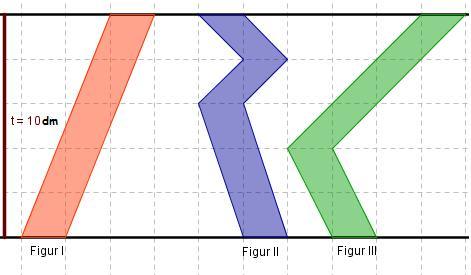
Übung zum Vertiefen
Ermittle den Flächeninhalt der vier Figuren I,II und III