Abschwächung der Gruppendefinition

Aussage

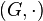Sei $(G,\cdot)$ eine Halbgruppe (d.h. Zweistellige Verknüpfung + Abgeschlossenheit + Assoziativität). Hat G rechtsinverse Elemente 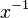$x^{-1}$ und ein rechtsneutrales Element $e$. Dann sind die rechtsinversen Elemente auch linksinvers und das rechtsneutrale Element auch linksneutral.

Beweis

Die Aussage enthält zwei Teilaussagen, die wir nacheinander beweisen:

1. Die rechtsinversen Elemente sind auch linksinvers.

2. Ein rechtsneutrales Element ist auch linksneutral.

Aspekte

• An gewissen Stellen in den Umformungen sind Klammern weggelassen worden. Denn wir wissen, dass die Verknüpfung assoziativ ist. Es gilt also:

Jede mögliche Klammerung darf gewählt werden. Denn jede mögliche Klammerung bildet auf dasselbe Element ab.

• Für ein Produkt endlich vieler Faktoren ist jede Klammerung äquivalent zu jeder anderen. (Verallgemeinertes Assoziativgesetz).

Zum Beispiel betrachten wir im Beweis der Teilaussage (1) ein Produkt von vier Faktoren. Hier verwenden wir, dass jede beliebige Klammerung äquivalent zu einer anderen frei wählbaren Klammerung ist. Das verallgemeinerte Assoziativgesetz kann induktiv gezeigt werden.

• Wir haben beim Beweis der Teilaussage (1) in den einzelnen Schritten sowohl, dass ein rechtsneutrales Element existiert, als auch, dass rechtsinverse Elemente existieren, verwendet. Ebenso die Assoziativität. Also sind alle diese Vorraussetzungen für die gemachten Folgerungen hinreichend. Allerdings ist die Frage offen, ob nicht mit weniger Vorraussetzungen und gewissen, noch nicht präzisierten Folgerungen das gleiche Ergebnis erreicht werden kann.
  

• Falls eine Halbgruppe ein linksneutrales Element und linksinverse Elemente enthält, kann analog gefolgert werden, dass ein linksneutrales Element auch rechtsneutral ist und, dass die linksinversen Elemente auch rechtsinvers sind.
  

• Da links- und rechtsinvers in einer Gruppe zusammenfällt. Fassen wir diese zwei Eigenschaften unter dem Begriff invers zusammen und sagen: Es existieren inverse Elemente.
  

• Im zweiten Teil der Aussage (2) verwenden wir, dass ein rechtsinverses Element auch linksinvers ist. Deswegen ist es gut und auch Absicht, dass wir zuerst (1) bewiesen haben. Da wir in Teilaussage (2) die Teilaussage (1) verwenden.
  

• G hat rechtsinverse Element, d.h. zu jedem Element 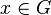$x \in G$ existiert ein Element aus G, welches wir mit 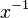$x^{-1}$ bezeichnen und für dieses gilt: 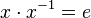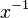$x \cdot x^{-1} = e$. $x^{-1}$ ist ein Element aus G. D.h. auch für dieses Element muss es ein rechtsinverses Element geben. Dieses bezeichnen wir mit 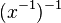$(x^{-1})^{-1}$. Es stellt sich heraus, dass $(x^{-1})^{-1} = x$ .

(Doppelte Invertierung eines Gruppenelements)

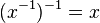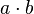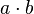• $a \cdot b$ ist auch ein Element aus G, weil die Verknüpfung $\cdot$ wieder nach G abbildet (Abgeschlossenheit/ innere Verknüpfung). Also muss es auch ein inverses Element zu $a \cdot b$ geben. Es stellt sich heraus, dass $(a \cdot b)^{-1} = b^{-1} \cdot a^{-1}$.

(Shoes and Socks)

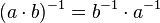• Wir haben gezeigt: Ist ein Gruppenelement ein rechtsneutrales Element der Gruppe, dann ist dieses Gruppenelement auch linksneutral. D.h. es könnte auch mehrere rechtsneutrale Elemente, und all diese sind dann auch linksneutral. Wie sich herausstellen wird, gibt es aber nur genau ein neutrales (rechts- und linksneutrales) Element. Genauso wird sich zeigen, dass das zu jedem Gruppenelement inverse Element eindeutig bestimmt ist.

(Eindeutigkeit des neutralen Elements und der inversen Elemente in einer Gruppe)