Zusammengesetzte Zufallsexperimente und Pfadregeln

Aufgabe 1:

Es wird zunächst ein klassischen Würfel und im Anschluss eine Münze geworfen.

a) Wie sieht das dazugehörige Baumdiagramm aus?

Zeichne es in dein Heft und vergleiche anschließend mit der Lösung hier

Baumdiagramm Würfel und Münzwurf

b) Kreuze alle Elemente an, die zum Ergebnisraum gehören:

({1;W}) ({1;Z}) ({2;W}) ({2;Z}) ({3;W}) ({3;Z}) ({4;W}) ({4;Z}) ({5;W}) ({5;Z}) ({6;W}) ({6;Z}) (!{1;1}) (!{2;3}) (!{4;2}) (!{5;1}) (!{W;Z}) (!{Z;W}) (!{0;W}) (!{W;1}) (!{Z;5}) (!{W;2}) (!{2;6}) (!{6;6})

c) Vervollständige dein Baumdiagramm aus Teilaufgabe a), indem du die einzelnen Wahrscheinlichkeiten an jeden Pfad schreibst.

Kontrollieren kannst du das Ergebnis mithilfe des folgenden Links:

Baumdiagramm mit den Wahrscheinlichkeiten

d) Berechne mithilfe der Pfadregeln die Wahrscheinlichkeiten der Ereignisse:

i) E₁: Es wird eine 1 gewürfelt:

Markiere im Baumdiagramm die zugehörigen Pfade gelb.

Kreuze die richtige Antwort an:

P(E₁) ist (!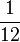$\frac{1}{12}$) ($\frac{1}{6}$) (!25%) (!$\frac{2}{3}$)

Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren:

Kontrolle i)

ii) E₂: Es wird Zahl geworfen

Markiere im Baumdiagramm die zugehörigen Pfade grün

Kreuze die richtige Antwort an:

P(E₂) ist (!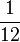$\frac{1}{6}$) (!$\frac{1}{12}$) (!$\frac{1}{3}$) (50%)

Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren:

Kontrolle ii)

iii) E₃: Es wird eine ungerade Augenzahl gewürfelt

Markiere im Baumdiagramm die zugehörigen Pfade blau

Kreuze die richtige Antwort an:

P(E₃) ist ($\frac{1}{2}$) (!35%) (!$\frac{1}{6}$) (!$\frac{3}{4}$)

Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren:

Kontrolle iii)

iv) E₄: Es wird mindestens eine 5 gewürfelt

Markiere im Baumdiagramm die zugehörigen Pfade rot

Kreuze die richtige Anwort an:

P(E₄) ist (!30%) ($\frac{1}{3}$) (!$\frac{1}{4}$) (!$\frac{1}{6}$)

Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren:

Kontrolle iv)

$\Leftarrow$ Zurück