Lernpfad2
|
Lernpfad
|
- Zeitbedarf: 35 Min.
- Material: Laufzettel und einen Stift
 Viel Spaß beim Bearbeiten des Lernpfads!
Viel Spaß beim Bearbeiten des Lernpfads!
1.Station: Multiplikation einer ganzen Zahl mit einem Bruch
Einführung:
Tom, Susi und Martin gehen zusammen Pizza essen. Jeder von ihnen isst drei der vorgeschnittenen  -Stücke seiner Pizza.
Welche Menge Pizza haben die drei insgesamt gegessen?
-Stücke seiner Pizza.
Welche Menge Pizza haben die drei insgesamt gegessen?
In der unten stehenden Zeichnung siehst du links die drei verschiedenen Pizzen von Tom, Susi und Martin. Rechts davon ist jedes Viertelstück der Dreien einzeln aufgelistet.
 |
 |
 |

|
 * 3 * 3 |
 + +  + +  + +  + +  + +  + +  + +  + + 
|
Hast du nun anhand der Zeichnung erkannt, welche Menge Pizza die drei zusammen essen??????
(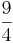 ) (!
) (!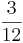 ) (!
) (!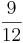 )
)
Diese Aufgabe soll dir helfen die Brüche bildlich vorzustellen!!
Kreuze an!!! Welche Rechenregel stimmt? (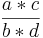 ) (!
) (!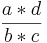 ) (!
) (!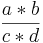 )
)
Die folgenden Aufgaben auf der nächsten Seite sollen dir zeigen, ob du die Regel verstanden hast und es anwenden kannst:
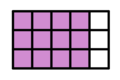

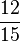
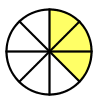

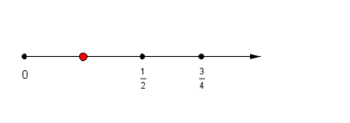
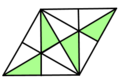
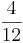


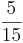

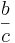 =
= 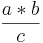
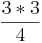 =
= 
