Calculators, Power Series and Chebyshev Polynomials
Of all the familiar functions, such as trigonometric, exponential and logarithmic functions, surely the simplest to evaluate are
polynomial functions. The purpose of this article is to introduce the concept of a power series, which can be thought of in the
first place as a polynomial function of infinite degree. In particular, we will deduce a series for 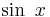 and will see how to
improve on the the most straightforward way of approximating its values. This simplest way uses the polynomials obtained by
truncating the power series. The improvement will involve Chebyshev polynomials, which are used in many ways for a similar
purpose and in many other applications, as well. When a calculator gives values of trigonometric or exponential or logarithmic
functions it is doing so by evaluating polynomial functions that are sufficiently good approximations. (For trigonometric
functions, the CORDIC algorithm is in fact often the preferred method of evaluation---the subject of another article here,
perhaps.)
and will see how to
improve on the the most straightforward way of approximating its values. This simplest way uses the polynomials obtained by
truncating the power series. The improvement will involve Chebyshev polynomials, which are used in many ways for a similar
purpose and in many other applications, as well. When a calculator gives values of trigonometric or exponential or logarithmic
functions it is doing so by evaluating polynomial functions that are sufficiently good approximations. (For trigonometric
functions, the CORDIC algorithm is in fact often the preferred method of evaluation---the subject of another article here,
perhaps.)
In the spirit of Felix Klein, there will be some reliance on a graphical approach.
Manipulations with geometric series
The geometric series 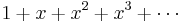 is the simplest power series. The sum of the series exists when
is the simplest power series. The sum of the series exists when 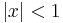 . In fact,
. In fact,
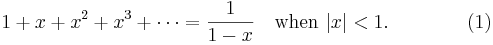
The general form of a power series is
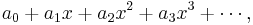
so the geometric series above is a power series in which all the coefficients 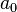 ,
, 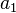 ,
, 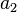 ,
, 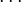 , are equal to 1. In
this case, since the series converges to
, are equal to 1. In
this case, since the series converges to 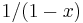 when
when 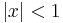 , we say that the function
, we say that the function 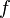 , where
, where
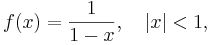
has the series expansion 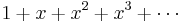 , or that
, or that 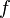 is represented by this series. We are interested initially to show some
other functions that can be represented by power series.
is represented by this series. We are interested initially to show some
other functions that can be represented by power series.
Many such functions may be obtained directly from the result in (1). For example, by replacing 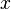 by
by 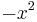 , we immediately have a
series representation for the function
, we immediately have a
series representation for the function 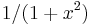 :
:
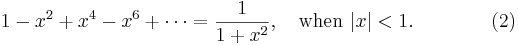
We can differentiate both sides of (1) to give a series representation of the function 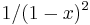 :
:
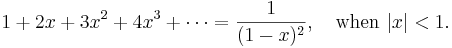
We can also integrate both sides of (1). Multiply through by 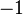 (for convenience), then write
(for convenience), then write 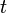 for
for 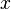 and integrate with respect
to
and integrate with respect
to 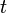 from 0 to
from 0 to 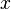 , where
, where 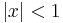 :
:
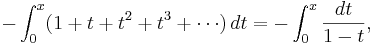
so
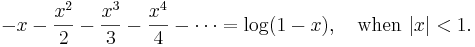
So this gives a series representation of the function 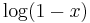 for
for 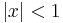 . In the same way, from (2),
. In the same way, from (2),
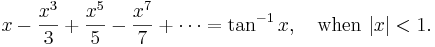
Much of what we have done here (and will do later) requires justification, but we can leave that to the textbooks.
The power series for the sine function
We will show next how to find a power series representation for 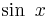 .
.
In general terms, we can write
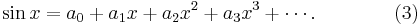
Put 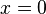 , and immediately we have
, and immediately we have 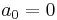 . Differentiate both sides
of (3):
. Differentiate both sides
of (3):
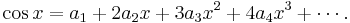
Again put 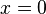 , giving
, giving 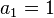 . Keep differentiating and putting
. Keep differentiating and putting 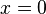 :
:
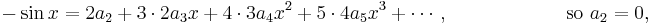
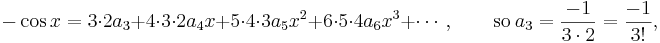
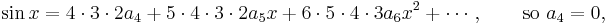
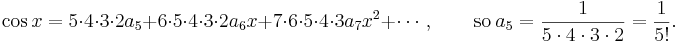
In this way, we can find a formula for all the coefficients 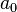 ,
, 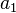 ,
, 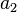 ,
, 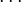 , namely,
, namely,
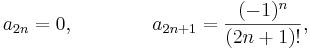
for 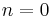 , 1, 2,
, 1, 2, 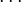 . (The coefficients of even index and those of odd index are specified separately.)
. (The coefficients of even index and those of odd index are specified separately.)
Thus
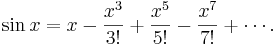
This is the power series representation that we were after. From the way we developed it, it is reasonable that the series will represent
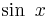 for values of
for values of 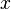 at and near 0 (say for
at and near 0 (say for 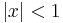 , as for all the earlier examples), so it is surprising to know that it can
be shown that the series represents
, as for all the earlier examples), so it is surprising to know that it can
be shown that the series represents 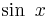 for all values of
for all values of 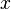 . Then partial sums of the series, obtained by stopping after
some finite number of terms, should give polynomial functions that can be used to find approximate values of the sine function, such as
you find in tables of trigonometric functions or as output on a calculator.
. Then partial sums of the series, obtained by stopping after
some finite number of terms, should give polynomial functions that can be used to find approximate values of the sine function, such as
you find in tables of trigonometric functions or as output on a calculator.

