Flächeninhalt ebener Figuren
- Entdecke auf dieser Seite, wie man die Flächeninhalte ebener Figuren berechnet!!
1.Wiederholung: Flächeninhalt von Rechtecken und Quadraten
- Du hast bereits gelernt, wie man den Flächeninhalt von Rechtecken und Quadraten berechnet.
- Erinnerst Du Dich noch daran?
- Bearbeite die folgende Aufgaben und Fülle die fehlenden Felder aus.
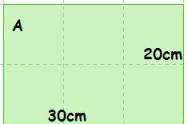 30cm
30cm  20cm = 600cm2
20cm = 600cm2
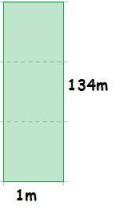 1m
1m  134m = 134m 2
134m = 134m 2
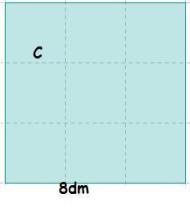 8dm
8dm  8dm = 64dm 2
8dm = 64dm 2
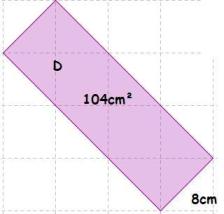 8cm
8cm  13cm = 104cm2
13cm = 104cm2
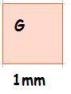 1mm
1mm  1mm= 1mm2
1mm= 1mm2
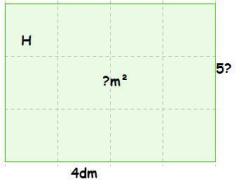 4dm
4dm  5m = 2m2
5m = 2m2
 a
a  b = ab
b = ab
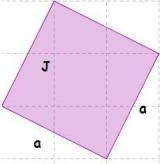 a
a  a = a2
a = a2
- Du hast alle Aufgabe richtig gelöst? Sehr gut!
- Dann kennst Du noch die Flächeninhaltsformel für Rechtecke und Quadrate.
- Überprüfe im nächsten Abschnitt, ob du richtig liegst.
Das solltest Du wissen
- Merke Dir die Berechnung für die Flächeninhalte des Rechtecks und Quadrates gut! Du wirst sie später wieder gebrauchen.
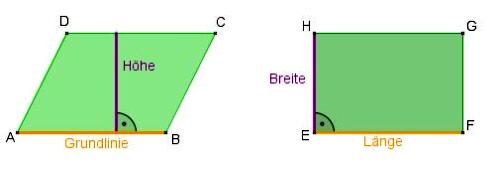
2.Das ist ja die Höhe!! Höhen ebener Figuren
- Du lernst in diesem Abschnitt, was die Höhen von Parallelogramm und Dreiecken sind.
- Bearbeite auch hier die Aufgaben sorgfältig, denn die Besonderheiten der Höhen wirst Du noch für die Flächeninhaltsberechnung brauchen!
2.1 Höhen im Parallelogramm
- Jetzt darfst Du konstruieren!
- Wenn Du die Geogebra Datei durch Klick auf den Button geöffnet hast, wirst Du ein Parallelogramm sehen.
- Bearbeite dazu die folgenden Aufgabenstellungen.
- Hinweis: In Geogebra werden Punkte in Großbuchstaben z.b. A,B,C ; Strecken und Geraden in Kleinbuchstaben a,b,c usw. angegeben.
- In der Menüleiste findest du wichtige Befehle, mit denen Du konstruieren kannst.
- Mach dich zunächst mit dem Programm vertaut!
Aufgabe:
- Zeichne von Punkt D aus eine senkrechte Gerade zur Parallelogrammseite a. Die Gerade wird automatisch benannt
- Schneide diese Gerade mit der Strecke a. Dabei erscheint ein grauer Punkt E
- Blende die Gerade aus. (Rechtsklick auf die Gerade und Befehl "Objekt anzeigen" deaktivieren)
- Erstelle nun eine Strecke zwischen Punkt C und E
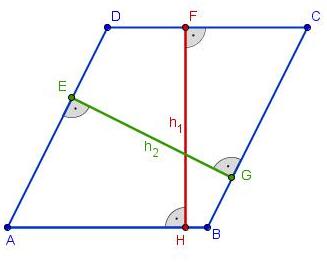
- Sehr schön, Du hast eine Höhe im Parallelogramm vom Eckpunkt D zur parallelen Seite a erstellt!
- Natürlich kann man von jedem anderen Punkt, der auf der Seite DC liegt, eine Höhe zur Seite AB konstruieren.
Zusammenfassung
- Merk dir die Definition für die Höhen im Parallelogramm gut. Du wirst sie später noch gebrauchen! Wenn du willst, dann kannst Du den Merkkasten in Dein Heft übetragen.
2.2 Höhen im Dreieck
- Auch hier darfst Du wieder konstruieren.
- Öffne wieder die Geogebra Datei durch Klick auf den Button. Konstruiere eine Höhe im dem vorgegebenen Dreieck, nach folgender Aufgabenstellung:
- Zeichne vom Punkt C aus eine senkrechte Gerade zur gegenüberliegenden Seite c des Dreiecks.
- Schneide wieder diese Gerade mit der Seite c.
- Blende die Gerade aus!
- Konstruiere eine Strecke zwischen dem erhaltenen Schnittpunkt und der Ecke C.
Sehr schön! Was Du konstruiert hast ist eine Höhe des Dreiecks vom Eckpunkt C aus, auf die gegenüberliegende Seite.
- 5. Bewege den Eckpunkt C nach Links und Rechts. Was passiert mit der Höhe?
Bewegt man den Eckpunkt C so weit, dass ein Basiswinkel (nicht der Winkel am Eckpunkt C) größer als 90° wird, so liegt die Höhe außerhalb des Dreiecks! Dies ist in stumpfwinkligen Dreiecken der Fall!
- So löst man das Problem:
- Konstruiere eine Gerade durch A und B
- Zeichne eine Senkrechte vom Punkt C zu dieser Geraden!
- Schneide diese Senkrechte Gerade mit der Geraden durch AB. Blende die Senkrechte Gerade wieder aus.
- Verbinde den erhaltenen Schnittpunkt mit C
- Was Du nun konstruiert hast, ist wieder eine Höhe vom Eckpunkt C aus. Doch diese kann auch außerhalb liegen!! Teste dies durch Bewegen von C!!
Zusammenfassung
- Auch die Eigenschaften der Höhen im Dreieck solltest du wissen. Daher wurden sie hier zusammengefasst. Wenn Du möchtest, kannst Du den Merkkasten in Dein Heft übrtragen.
 |
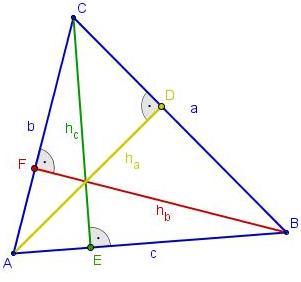
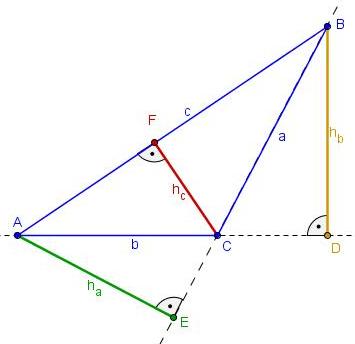
Die Höhe im Dreieck ist der Abstand von einem Eckpunkt des Dreiecks zur gegenübeliegenden Seite. Die Punkte D,E,F nennt man Höhenfußpunkte
|
3.Flächeninhalt Parallelogramm
3.1 Einstieg
- Lass uns hier gemeinsam die Formel für den Flächeninhalt des Parallelogramms erarbeiten. Du wirst sehen, es ist gar nicht so schwer!
- Hier siehst Du eine Möglichkeit, wie man die Flächeninhaltsformel von Parallelogrammen herleiten kann
| Verschiebe das Rechteck und beobachte was passiert! Bearbeite dazu die folgenden Fragen:
|
 |
Wir haben das Parallelogramm in ein Trapez und ein rechtwinkliges Dreieck zerlegt. Anschließend wurd das Trapez durch Verschiebung des Dreiecks zum Rechteck ergänzt. Diese Verschiebung stellt eine Kongruenzabbildung dar. Das erhaltene Rechteck und das Ausgangsdreieck sind damit zerlegungsgleich und besitzen somit den gleichen Flächeninhalt.
|
3.2 Flächeninhaltsformel des Parallelogramms
- Auch die Formel für die Berechnung des Flächeninhalts kannst Du hier erarbeiten.
- Fülle zunächst die Lücken aus. und Übertrage anschließend den Merkkasten in Dein Heft!
 |
Länge(Rechteck) = Grundseite (Parallelogramm) Der Flächeninhalt des Parallelogramms ist definiert als: |
3.3 Zusammenfassung:
- Merk dir sehr gut, wie man den Flächeninhalt von Parallelogrammen berechnet. Du wirst später darüber abgefragt!
 |
Den Flächeninhalt eines Parallelogramms berechnet man durch: FParallelogramm = g |
3.4 Vertiefen und Erweitern
Bitte bearbeite die folgenden Aufgaben.
Variante zur Herleitung
Eine weitere Lösungsidee ist in der nächsten Darstellung verborgen:
Aufgabenstellung:
In diesem Fall werden nicht die Parallelogrammseiten betrachtet, die auf den Parallelen Geraden liegen, sondern das andere Seitenpaar. Entsprechend wird die dazugehörige Höhe zur Flächenberechnung gewählt! |
 |
Zur Berechnung der Flächeninhaltsformel kann jede Seite des Parallelogrammes als Grundseite und die zugehörige Höhe genommen werden. |
Flächeninhaltsgleiche Parallelogramme
| Erkläre, warum die abgebildeten Parallelogramme den gleichen Flächeninhalt, wie das rote Rechteck haben.
Du kannst die Parallelogramme mit dem Schieberegler ziehen.
Tipp: Du kannst auch die Höhe anzeigen lassen.
Die Parallelogramme haben den gleichen Flächeninhalt wie das rote Rechteck, da sie dieselbe Grundseite besitzen. Auch die Höhe ist in allen Parallelogrammen (wie auch im Rechteck) gleich, das die verschiebbaren Seiten auf der gleichen Parallele zur Grundseite liegen und somit den gleichen Abstand zur Grundseite besitzen.
|
Das Höhenproblem
- Du hast in der Herleitungsvariante erarbeitet, dass man immer jede Parallelogrammseite als Grundseite verwenden kann. Dies ist auch für das nächste Parallelogramm der Fall, auch wenn eine Höhe außerhalb des Parallelogramms liegt, wenn man diese einzeichnet.
- Wie könnte man für dieses spezielle Parallelogramm die Formel für den Flächeninhalt von Parallelogrammen trotzdem beweisen? dazu die außerhalb des Parallogramms liegende Höhe!!
|
Aufgabenstellung: Verfolge die Schritte!
Die Mittelparallele halbiert das gelbe Parallelogramm. Dabei wird die Höhe halbiert, jedoch die Grundseite bleibt erhalten.
Fgesamt ist der Flächeninhalt des Ausgangsparallelogramms. F1 und F2 sind die Flächeninhalte der Teilparallelogramme, die durch die Zerlegung mit der Mittelparallele entstehen. Es gilt:
|
3.5 Übung
- In der Tabelle sind Werte verschiedener Größen von Parallelogrammen angegeben.
- Arbeitsauftrag:
- Berechne die fehlende Werte und Fülle die Lücken aus! Runde sinnvoll!
| Parallelogramm | g1 | h1 | Flächeninhalt | g2 | h2 |
|---|---|---|---|---|---|
| A | 3 cm | 2cm | 6 cm² | 2,24 cm | 2,68cm |
| B | 3 cm | 3cm | 9 cm² | 3,6cm | 2,5cm |
| C | 4 cm | 4 cm | 16 cm² | 4,47cm | 3,57cm |
| D | 6cm | 5 cm | 30cm² | 5,39 cm | 5,57cm |
| E | 6 cm | 3,01cm | 18,1cm² | 3,62cm | 5cm |

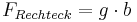
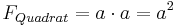


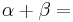 180°
180°
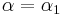
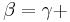 90° bzw.
90° bzw.
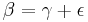
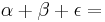 180°
180°

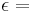 90°
90° 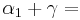 90°
90°