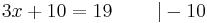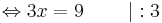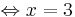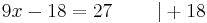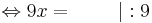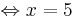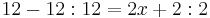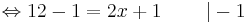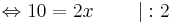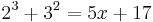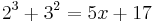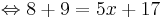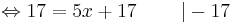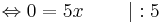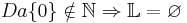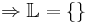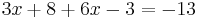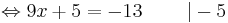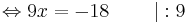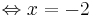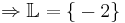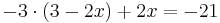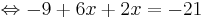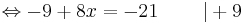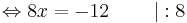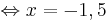Algebra: Gleichungen
Aus DMUW-Wiki
Deine neue Lieblings-Merkregel zum Umformen von Termen und Gleichungen:
Rechne immer Klammer vor Punkt vor Strich!
|
Wie bei einer Waage müssen beide Seiten der Gleichung immer im Gleichgewicht sein. Dies erreichst du durch Äquivalenzumformungen, mit denen du beide Seiten der Gleichung einheitlich umstellst, ohne dass sich der Wert der Gleichung ändert. |
Wende diese Regel nun auf die folgenden Aufgaben an. Beachte immer die Grundmenge, die rechts steht.
Wenn du dir sicher bist, welche Äquivalenzumformung als nächstes kommt, darfst du durch Markieren des grauen Feldes den jeweils nächsten Schritt sichtbar machen!
Erst ganz am Ende kannst du dann dein Ergebnis durch Klick auf "Lösung anzeigen" überprüfen.
- 3x + 10 = 19 | - 10
 3x = 9 | : 3
3x = 9 | : 3
 x = 3
x = 3
- 9x - 18 = 27 | + 18
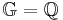
 9x = 45 | : 9
9x = 45 | : 9
 x = 5
x = 5
- 12 - 12 : 12 = 2x + 2 : 2
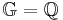
 12 - 1 = 2x + 1 | - 1
12 - 1 = 2x + 1 | - 1
 10 = 2x | : 2
10 = 2x | : 2
 x = 5
x = 5
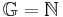
 8 + 9 = 5x + 17
8 + 9 = 5x + 17
 17 = 5x + 17 | - 17
17 = 5x + 17 | - 17
 0 = 5x | : 5
0 = 5x | : 5
 x = 0 ... wirklich?
x = 0 ... wirklich?
- 3x + 8 + 6x - 3 = -13
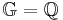
 9x + 5 = -13 | - 5
9x + 5 = -13 | - 5
 9x = -18 | : 9
9x = -18 | : 9
 x = -2
x = -2
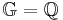
 -9 + 6x + 2x = -21
-9 + 6x + 2x = -21
 -9 + 8x = -21 | + 9
-9 + 8x = -21 | + 9
 8x = -12 | : 8
8x = -12 | : 8
 x = -1,5
x = -1,5