Praktische Grenzen der Berechenbarkeit
Inhaltsverzeichnis |
Zuordnungsquiz
Ordne den Funktionsnamen die zugehörigen Graphen und Terme zu!
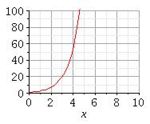 |
Exponentialfunktion | 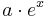
|
 |
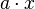 |
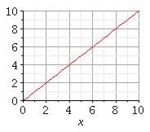
Lineare Funktion |
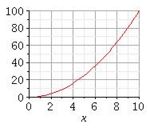 |
Potenzfunktion | 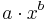
|
Türme von Hanoi
Aufgabe
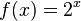
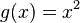
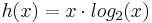
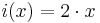
Ab welchem 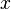 ist das exponentielle Wachstum schlechter als das Polynomielle?
ist das exponentielle Wachstum schlechter als das Polynomielle?

Also ist 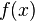 schlechter als
schlechter als 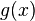 für
für 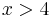 ,
,
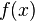 schlechter als
schlechter als 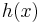 für
für 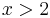 ,
,
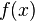 schlechter als
schlechter als 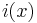 für
für 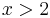 .
.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| f(x) | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Aufgabe
Wie viele Knoten hat ein Spielbaum, bei dem jeder Halbzug (das heißt ein Zug von Spieler A oder B) 5 Zugmöglichkeiten hat und ein Spiel im Schnitt 60 Halbzüge hat. Kann man diesen Spielbaum auf einer handelsüblichen Festplatte speichern, wenn pro Knoten 1 Byte Speicherplatz benötigt wird?
Für die Speicherung eines solchen Spielbaumes würde man ungefähr 8*10^35 GB benötigen. Eine Studie von IDC hat für 2008 prognostiziert, dass der weltweit verfügbare Speicherplatz 2,25*10^21 Bits beträgt. Es ist also nicht möglich einen solchen Spielbaum zu speichern.

