Volumen des Zylinders
Hier werden wir uns nun um das Volumen des Zylinders kümmern. Du benötigst dafür dein Schulheft und Stifte
1. Aufgabe
Wir haben im ersten Lernpfad dreiseitige Prismen wiederholt. Dort haben wir auch festgestellt, dass die Formel für das Volumen eines Körpers in der Grundform immer gleich ist, nämlich  . Diese Formle gilt ebenso für unseren neune Körper Zylinder.
Nun benötigen wir aber noch die Grundfläche G. Diese besteht bei unserem Zylinder aus einem Kreis. Der Flächeninhalt des Kreises lässt sich mit
. Diese Formle gilt ebenso für unseren neune Körper Zylinder.
Nun benötigen wir aber noch die Grundfläche G. Diese besteht bei unserem Zylinder aus einem Kreis. Der Flächeninhalt des Kreises lässt sich mit 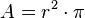 darstellen.
Also können wir die Formel für das Zylindervolumen zusammenfügen:
darstellen.
Also können wir die Formel für das Zylindervolumen zusammenfügen: 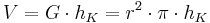 .
.
2. Aufgabe
Nun sollst du dein Schulheft zur Hand nehmen und mit Hilfe der folgenden Anleitung einen Zylinder mit dem Radius 3cm und der Höhe 7cm in das Heft zeichnen. Schreibe darüber als Überschrift "Volumen des Zylinders".
| Schritt 1 | ||
|---|---|---|
| Als erstes lässt du ca. 10cm Platz und zeichnest dann eine waagrechte Linie mit der Länge 2r also 6cm. |
| Schritt 2 | ||
|---|---|---|
| Nun zeichnest du eine senkrechte Linie im Mittelpunkt der ersten Linie mit je 1,5cm Länge (nach oben und unten). |
| Schritt 3 | ||
|---|---|---|
| Als nächstes verbindest du die vier Eckpunkte zu einem schrägen Kreis bzw. zu einer Ellipse. |
| Schritt 4 | ||
|---|---|---|
| Jetzt trägst du an den zwei Eckpunkten rechts und links jeweils die Höhe des Zylinders (7cm) senkrecht an und verbindest die Enden. |
| Schritt 5 | ||
|---|---|---|
| Nun wiederholen wir Schritt 2 und 3 und zeichnen wieder eine Senkrecht im Mittelpunkt der ebene gezeichneten Strecke mit je 1,5cm nach oben und unten. Diese vier Eckpunkte verbinden wir wieder zu einem schrägen Kreis. |
| Schritt 6 | ||
|---|---|---|
| Nun radieren wir noch unnötig Hilfslinien wieder weg. |

