Seite 5

Teilaufgabe f)

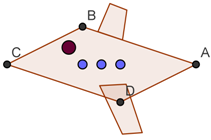Schauen wir uns jetzt den Körper des Flugzeugs an..
1. Fülle dazu den Lückentext aus, indem du die verdrehten Wörter entschlüsselst!

Eine Figur die durch Drehung um 180° auf sich selbst abgebildet wird, heißt punktsymmetrisch zu einen Punkt Z. Der Drehpunkt Z wird auch Symmetriezentrum genannt. Er ist der einzige Punkt der auf sich selbst abgebildet wird und ist somit ein Fixpunkt.
Die Punktsymmetrie ist ein Sonderfall der Drehsymmetrie.

2. Entscheide, welche Aussagen auf die geometrische Figur des Flugzeugs zutreffen! Es können mehrere Antworten richtig sein!

1. Welche Aussagen kannst du über die Seiten des Körpers treffen? Gegenüberliegende Seiten sind gleich lang Alle vier Seiten sind gleich lang Gegenüberliegende Seiten sind parallel 2. Was trifft auf die Diagonalen zu? Die Diagonalen stehen senkrecht aufeinander Die Diagonalen halbieren sich gegenseitig Die Diagonalen sind gleich lang 3. Welche geometrische Figur stellt der Körper des Flugzeugs dar? Trapez Parallelogramm Drache 4. Ist der Körper des Flugzeugs symmetrisch? Der Körper ist punktsymmetrisch Der Körper ist drehsymmetrisch Es liegt keine Symmetrie vor 5. Welche Koordinaten hat das Symmetriezentrum? (3|3.5) (3.5|3) (3|3) Punkte: 0 / 0

→Auf zur letzten Teilaufgabe!