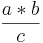Lernpfad3
|
Lernpfad
|
- Zeitbedarf: 35 Min.
- Material: Laufzettel und einen Stift
 Viel Spaß beim Bearbeiten des Lernpfads!
Viel Spaß beim Bearbeiten des Lernpfads!
1.Station: Multiplikation einer ganzen Zahl mit einem Bruch
Einführung:
Tom, Susi und Martin gehen zusammen Pizza essen. Jeder von den Dreien isst drei seiner in  -Stücke geschnittenen Pizza. Also isst jeder
-Stücke geschnittenen Pizza. Also isst jeder  seiner Pizza!!!
seiner Pizza!!!
Kreuze nun den richtigen Rechenweg an und klicke auf prüfen!, um zu sehen, ob du Recht hast.
(!3 *  =
= 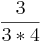 =
= 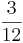 )
)
(3 *  =
= 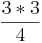 =
= 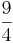 = 2
= 2  )
)
(3 *  =
= 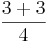 =
=  = 1
= 1  )
)
Versuche nun die Aufgaben zu lösen und klicke danach auf Prüfen!!! Falsche Antworten werden mit rot angezeigt, richtige mit grün!! Es können auch mehrere Lösungen möglich sein!!!
2 *  = (
= ( ) (
) ( ) (!
) (!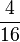 )
)
5 *  = (3) (!
= (3) (!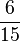 ) (!10)
) (!10)
6 *  = (8) (
= (8) (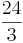 ) (!
) (!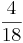 )
)
Multiplikation einer ganzen Zahl mit einem Bruch
Kannst du die Rechenregeln jetzt auch verbal ausdrücken???
Finde die unverdrehte Lösung zu den verdrehten Wörtern!
Der Zähler wird mit der ganzen Zahl multipliziert.
Der Nennerbleibt stehen.
Danach wird das Ergebnis soweit wie möglich gekürzt und in einen gemischten Bruch umgewandelt!!!
Hier gilt das Kommutativgesetz.

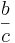 =
=