Algebra: Potenzen und Potenzfunktionen

Graph 1

Graph 2

Graph 3

Graph 4

1. Klicke auf die jeweils zutreffenden Aussagen!

Graph 1	Graph 2	Graph 3	Graph 4
				$y = x^2$
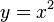→	Alle Parabeln mit positiven, geraden Exponenten beschreiben diese Funktionen.
				achsensymmetrisch
→	Parabeln und Hyperbeln gerader Ordnung sind symmetrisch zur x-Achse.
				Parabel ungerader Ordnung
→	Diese Parabeleln haben positive, ungerade Exponenten.
				$\mathbb{D} = \mathbb{R}\setminus \{ 0\}$ ; $\mathbb{W} = \mathbb{R}\setminus \{ 0\}$
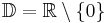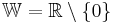→	Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!
				Asymptoden x = 0; y = 0
→	Diese Graphen sind punktsymmetrisch und haben somit die beiden Achsen als Asymptoten.
				$\mathbb{D} = \mathbb{R}\setminus \{ 0\}$ ; $\mathbb{W} = \mathbb{R}^+$
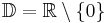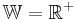→	Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!
				Hyperbel gerader Ordnung
→	Diese haben negative, gerade Exponenten.
				$y = x^{-7}$
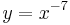→	Alle Hyperbeln mit negativen, ungeraden Exponenten beschreiben diese Funktionen.
				punktsymmetrisch
→	Parabeln und Hyperbeln ungerader ordnung sind punktsymmetrisch zum Ursprung
				Scheitelpunkt im Ursprung
→	Die Koordinaten des Scheitelpunkts sind (0|0).
				Symmetriepunkt im Ursprung
→	Die Koordinaten des Symmetriepunkts sind (0|0).
				$y = x^5$
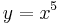→	Alle Parabeln mit positiven, ungeraden Exponenten beschreiben diese Funktionen.
				$\mathbb{D} = \mathbb{R}$
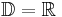→	Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!

Punkte: 0 / 0