Einstieg
Inhaltsverzeichnis |
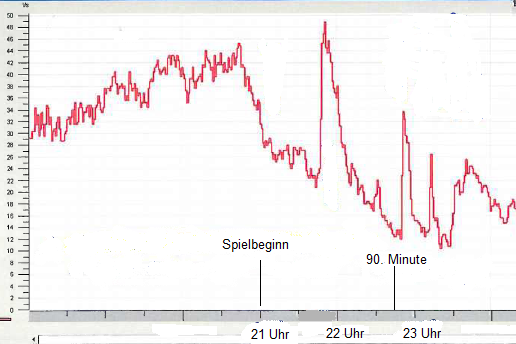
Fußball-Weltmeisterschaft 2006 - Wasserverbrauch
Während der Fußball-Weltmeisterschaft 2006 konnten die Wasserversorger während der Spiele eine interessante Entdeckung machen.
Die WVV (Würzburger Versorgungs- und Verkehrs-GmbH) hat im Versorungsgebiet Würzburg-Heuchelhof während des Halbfinalspiels zwischen Deutschland und Italien folgende Aufzeichnungen gemacht. Aber sieh dir das selbst einmal an.
An der x-Achse kannst du den Zeitverlauf ablesen und an der y-Achse den Wasserverbrauch in Litern pro Sekunde. Als Hilfe ist der Spielbeginn und das Ende der regulären Spielzeit angezeigt.
Wie lässt sich der Verlauf der Kurve erklären?
Bevor wir auf die Lösung der Frage eingehen, richten wir unser Augenmerk auf die Halbzeitpause.
Halbzeitpause
Kleine Hilfen erleichtern uns die Arbeit:
{{
Wir arbeiten mit etwas vereinfachten Daten, die sich jedoch auf die Graphik oben beziehen. Ebenso gleichen wir die Koordinaten-Achsen einander an, indem wir die y-Werte in Hektolitern (hl) und die x-Achse in Minuten (min) angeben. (1 Hektoliter = 100 Liter)
}}
Nun kann es losgehen!
Die folgenden Daten stehen zum Wasserverbrauch in der Halbzeitpause zur Verfügung:
| A | B | C | D | E | F | G | H | K | |
|---|---|---|---|---|---|---|---|---|---|
| Verbrauch in hl | 13,2 | 21 | 26,4 | 29,4 | 30,075 | 29,4 | 26,4 | 21 | 13,2 |
| Zeit in min | 0 | 2 | 4 | 6 | 7,5 | 9 | 11 | 13 | 15 |
Aufgabe 1
a) Stelle die Daten aus der Tabelle in einem Koordinatensystem dar. Verschiebe dazu die Punkte A bis K mit der Maus an die richtige Stelle.
Beachte die Beschriftung der x- und y-Achse.
GEOGEBRA-APPLET
Jetzt kannst du durch Ablesen an der Funktinon die Aufgabenteile a) und b) lösen:
b) In welcher Minute der Halbzeitpause ist der Wasserverbrauch am höchsten?
c) Wie hoch ist der Verbrauch zu diesem Zeitpunkt?
Rückblick
Die Kurve, die wir gemeinsam entwickelt haben, gehört zu den Funktionen.
Du kennst bereits Lineare Funktionen. Dein Wissen dazu kannst du in dem Lückentext überprüfen und wiederholen.
Die Funktionen, die wir gemeinsam entwickelt haben, nennt man quadratische Funktion.
Ihr Funktionsterm hat die Form ax². Sie zählen daher zu den quadratischen Funktionen. Die Graphen quadratischer Funktionen unterscheiden sich stark von den Graphen linearer Funktionen.
|
Merke:
Die Graphen von Funktionen mit der Funktionsgleichung Sie sind symmetrisch zur y-Achse. Der Punkt Ist |

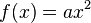 heißen Parabeln.
heißen Parabeln.
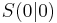 heißt Scheitel der Parabel und ist der tiefste Punkt.
heißt Scheitel der Parabel und ist der tiefste Punkt.
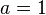 heißt der Graph Normalparabel.
heißt der Graph Normalparabel.

