Abbildung durch zentrische Streckung

Lernpfad Abbildung durch zentrische Streckung

1. Station: Ähnlichkeitsabbildung

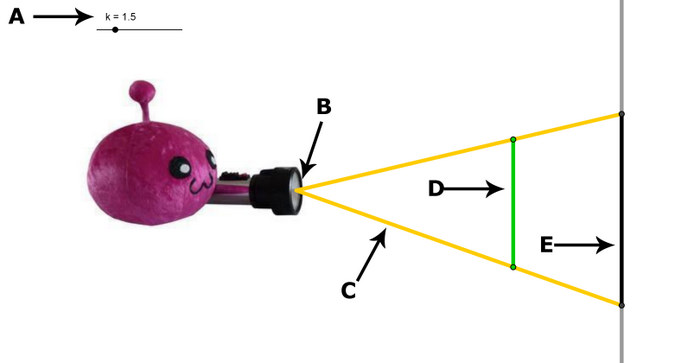
Hier siehst du Panto mit einer Taschenlampe. Schalte die Taschenlampe ein, dann leuchtet

sie direkt auf einen grünen Strohhalm. An der Wand entsteht dabei ein Schatten.

Verschiebe Panto näher an den Strohhalm heran, oder weiter von dem Strohhalm weg.

Lies die folgenden Beobachtungen konzentriert durch und hake die richtigen Aussagen ab:

1. Wie ändert sich der Schatten durch das Verschieben?

	Je näher Panto mit der Taschenlampe auf den Strohhalm leuchtet, desto größer ist der Schatten.
	Je näher Panto mit der Taschenlampe auf den Strohhalm leuchtet, desto kleiner ist der Schatten.
	Je weiter Panto mit der Taschenlampe von dem Strohhalm entfernt ist, desto kleiner ist der Schatten.
	Je weiter Panto mit der Taschenlampe von dem Strohhalm entfernt ist, desto größer ist der Schatten.

Punkte: 0 / 0

Der Strohhalm wird als Urbild und der Schatten als Bild bezeichnet.

Wie man sieht haben der Strohhalm und der Schatten verschiedene Größen, doch sie sind sich ähnlich.

Deshalb spricht man von einer Ähnlichkeitsabbildung.

Die Vergrößerung geht von einem Zentrum, in unserem Beispiel der Taschenlampe, aus. Man spricht hierbei von

einer zentrischen Streckung. Das Streckungszentrum wird mit Z bezeichnet.

Urbild, Bild und Streckungszentrum liegen auf den Lichtstrahlen, die von der Taschenlampe ausgehen. Diese

Lichtstrahlen sind Halbgeraden.

2. Station: Streckungsfaktor

In dem nächsten Fall ist das Urbild ein Dreieck, dass du zentrisch strecken kannst, indem du an dem Schieberegler ziehst.

Der Schieberegler durchläuft die positiven Zahlen von k=0 bis k=3.

Was verändert sich? Orientiere dich dabei an diesen Fragen: Auf welcher Seite von Z liegen das Urbild und das Bild? (auf derselben Seite) (!auf verschiedenen Seiten) Was liegt bei k>1 vor? (eine Vergrößerung) (!eine Verkleinerung) (!die Identität) Was liegt bei 0<k<1 vor? (!eine Vergrößerung) (eine Verkleinerung) (!die Identität) Was liegt bei k=1 vor? (!eine Vergrößerung) (!eine Verkleinerung) (die Identität) Was passiert wenn k=0 ist? (es erfolgt keine zentrische Streckung) (!es erfolgt eine zentrische Streckung)

Was sind die Unterschiede, wenn ihr dieses Dreieck zentrisch streckt? Dieses mal durchläuft der

Schieberegler die negativen Zahlen von k=-3 bis k=0.

Was verändert sich? Orientiere dich dabei an diesen Fragen: Auf welcher Seite von Z liegen das Urbild und das Bild? (!auf derselben Seite) (auf verschiedenen Seiten) Was liegt bei k< -1 vor? (eine Vergrößerung) (!eine Verkleinerung) (!die Identität) (!eine Spiegelung) Was liegt bei 0>k> -1 vor? (!eine Vergrößerung) (eine Verkleinerung) (!die Identität) (!eine Spiegelung) Was liegt bei k= -1 vor? (!eine Vergrößerung) (!eine Verkleinerung) (!die Identität) (eine Spiegelung)

Um herauszufinden was das k bedeutet, musst du dir jetzt bei dieser zentrischen Streckung anschauen, wie

sich die Streckenlängen verändern, wenn du k veränderst. Dazu musst du dir die Streckenlängen anzeigen lassen.

Zur Hilfe orientiere dich an dieser Frage:

Was ist der Unterschied zwischen der Länge der Bildstrecke zur Urbildstrecke?

Hier kannst du deine Vermutung mit der von Dia vergleichen:

[Lösung anzeigen][Lösung ausblenden]

Die Bildstrecken sind jeweils |k|-mal so lang wie die Urbildstrecken.

k bezeichnet man als den Streckungsfaktor. Er gibt den Maßstab an, in dem das Bild vergrößert wurde.

3. Station: Berechnung der Streckenlängen und des Streckungsfaktors

Wie ihr in der 2. Station schon herausgefunden habt ist die Bildstrecke |k|-mal so lang wie die Urbildstrecke.

Geometrisch bedeutet dies: ZB' = |k| ∙ ZB

5. Station: Übung

Das Bild zeigt eine zentrische Streckung.

Vorsicht: Die Nummerierung im Bild stimmt nicht mit der Nummerierung der Kreuzworträtselkästchen überein! Lies die Frage genau durch, um zu wissen nach welcher Nummer gefragt ist!!!

Streckungsfaktor	Was zeigt die 1?
Streckungszentrum	Was zeigt die 2?
Halbgerade	Was zeigt die 3?
Urbild	Was zeigt die 4?
Bild	Was zeigt die 5?