Abbildung durch zentrische Streckung
 Lernpfad
|
2. Station: Streckungsfaktor
3. Station: Berechnung der Streckenlängen und des Streckungsfaktors
4. Station: Zusammenfassung
5. Station: Übungen
6. Station: Wissenswertes
1. Station: Ähnlichkeitsabbildung
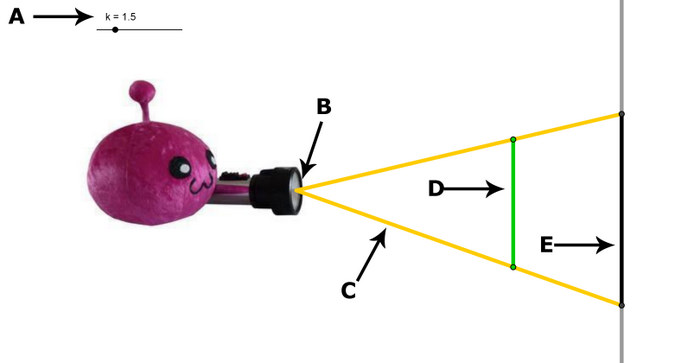
- Hier siehst du Panto mit einer Taschenlampe. Schalte die Taschenlampe ein, dann leuchtet
- sie direkt auf einen grünen Strohhalm. An der Wand entsteht dabei ein Schatten.
- Verschiebe Panto näher an den Strohhalm heran, oder weiter von dem Strohhalm weg.
- Lies die folgenden Beobachtungen konzentriert durch und hake die richtigen Aussagen ab:
Wie ändert sich der Schatten durch das Verschieben? (Je näher Panto mit der Taschenlampe auf den Strohhalm leuchtet, desto größer ist der Schatten.) (!Je näher Panto mit der Taschenlampe auf den Strohhalm leuchtet, desto kleiner ist der Schatten.) (Je weiter Panto mit der Taschenlampe von dem Strohhalm entfernt ist, desto kleiner ist der Schatten.) (!Je weiter Panto mit der Taschenlampe von dem Strohhalm entfernt ist, desto größer ist der Schatten.)
- Lies den Text genau durch. Am Ende wirst du darüber abgefragt.
- Der Strohhalm wird als Urbild und der Schatten als Bild bezeichnet.
- Wie man sieht haben der Strohhalm und der Schatten verschiedene Größen, doch sie sind sich ähnlich.
- Deshalb spricht man von einer Ähnlichkeitsabbildung.
- Die Vergrößerung geht von einem Zentrum, in unserem Beispiel der Taschenlampe, aus. Man spricht hierbei von
- einer zentrischen Streckung. Das Streckungszentrum wird mit Z bezeichnet.
- Urbild, Bild und Streckungszentrum liegen auf den Lichtstrahlen, die von der Taschenlampe ausgehen. Diese
- Lichtstrahlen sind Halbgeraden.
2. Station: Streckungsfaktor
- In dem nächsten Fall ist das Urbild ein Dreieck, dass du zentrisch strecken kannst, indem du an dem Schieberegler ziehst.
- Der Schieberegler durchläuft die positiven Zahlen von k=0 bis k=3.
| Was verändert sich? Orientiere dich dabei an diesen Fragen:
|
- Was sind die Unterschiede, wenn du dieses Dreieck zentrisch streckst? Dieses mal durchläuft der
- Schieberegler die negativen Zahlen von k=-3 bis k=0.
| Was verändert sich? Orientiere dich dabei an diesen Fragen:
|
- Um herauszufinden was das k bedeutet, musst du dir jetzt bei dieser zentrischen Streckung anschauen, wie
- sich die Streckenlängen verändern, wenn du k veränderst. Dazu musst du dir die Streckenlängen anzeigen lassen.
| Was verändert sich? Orientiere dich dabei an diesen Fragen:
|
- Die Werte, die sich aus der Änderung von k ergeben, wurden in zwei Tabellen zusammengefasst.
- In der linken sind die Werte für k von 2 bis 0, in der rechten für k von -2 bis 0.
- Arbeitsauftrag:
- 1. Betrachte zunächst nur die linke Tabelle und stelle eine Vermutung auf, wie sich die Länge von ZB' ändert im Vergleich zur Länge von ZB?
- (Tipp: Betrachte auch den Wert von k!)
- 2. Vergleiche die Zeilen mit der selben Hintergrundfarbe! Was haben sie gemeinsam? Was sind die Unterschiede?
|
|
- Hier kannst du deine Vermutung mit der von Dia vergleichen:
1. 
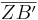ist k-mal so lang wie 
.
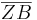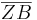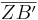und bleiben gleich, wenn sich das Vorzeichen von k ändert.
- Dia ist nach ihren Vermutungen total verwirrt. Sie versteht nicht warum der Wert von ZB' gleich bleibt, wenn sich das Vorzeichen von k ändert.
- Vielleicht kannst du ihr helfen, indem du ihre Fragen beantwortest:
- Prima! Dank dir versteht jetzt Dia, wie die Werte für ZB' entstehen.
- Mit deiner Hilfe und ihrer Vermutungen kann sie eine allgemeingültige Aussage machen.
- Teste durch Einsetzen der richtigen Wörter, ob auch du dahinter gekommen bist:
Die Länge von ZB ist |k|-mal so lang wie die Länge von ZB'.
- Hier siehst du was das k bedeutet. Merke es dir, denn später wirst du darüber abgefragt!
- k bezeichnet man als den Streckungsfaktor. Er gibt den Maßstab an, in dem das Bild vergrößert wurde.
3. Station: Berechnung der Streckenlängen und des Streckungsfaktors
- Wie du in der 2. Station schon herausgefunden hast ist die Bildstrecke |k|-mal so lang wie die Urbildstrecke.
- Geometrisch bedeutet dies für einen beliebigen Punkt P: ZP' = |k| ∙ ZP
- Daraus folgt: k=
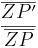
- Ob dies auch zur Berechnung von Strecken, die nicht durch den Punkt Z verlaufen, gilt, kannst du durch Umformung herausfinden.
- Setze dafür den richtigen Ausdruck in die passende Lücke:
 |
P'Q' = |k| ∙ PQ |
4. Station: Zusammenfassung
- Hier siehst du alles, was du bisher herausgefunden hast zusammengefasst.
- Schreibe dir diese Zusammenfassung in dein Heft.
Abbildungsvorschrift der zentrischen Streckung
Wenn eine Vergrößerung von einem Zentrum ausgeht, dann spricht man von einer zentrischen Streckung.
Sie wird festgelegt durch Angabe eines Streckungszentrums Z und eines Streckungsfaktors k. (Kurz: )
Der Urpunkt P, der Bildpunkt P' und das Streckungszentrum Z liegen auf einer Geraden.
Es gilt: ZP' = |k| ∙ ZP
Bei |k|>1 liegt eine Vergrößerung, bei 0<|k|<1 eine Verkleinerung vor.
Wenn k=1 ist liegt die Identität vor, bei k= -1 eine Spiegelung.
Für k>0 gilt: Urpunkt und Bildpunkt liegen auf der gleichen Seite von Z.
Für k<0 gilt: Urpunkt und Bildpunkt liegen auf verschiedenen Seiten von Z.
5. Station: Übungen
1. Aufgabe
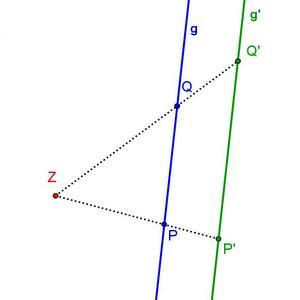
- Das Bild zeigt eine zentrische Streckung.
 |
|
2. Aufgabe
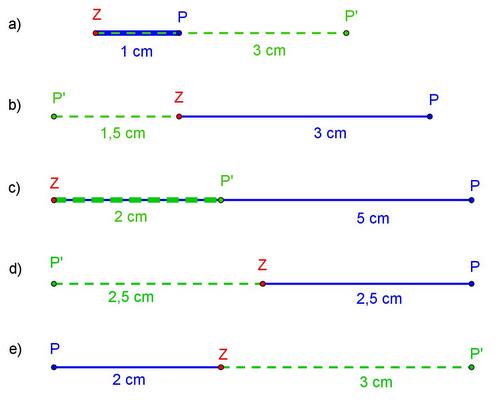
- Berechne den Streckungsfaktor k in deinem Heft. Ordne danach die richtige Lösung zu:
 |
a) k= 3 |
3. Aufgabe
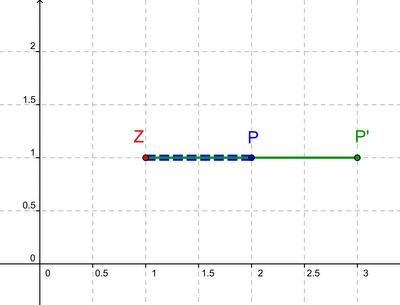
- Trage für jede Teilaufgabe in einem Koordinatensystem die Ur- und Bildpunkte ein, verbinde sie wenn möglich
- und führe die zentrische Streckung mit gegebenem Zentrum und Streckungsfaktor durch.
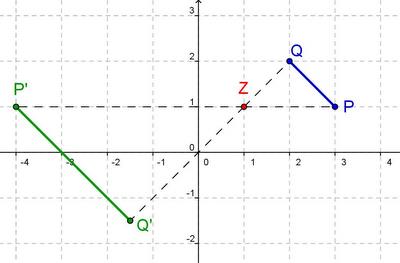
- a) Z(1|1), k= 2, P(2|1)
- b) Z(1|1), k= -2.5, P(3|1), Q(2|2)
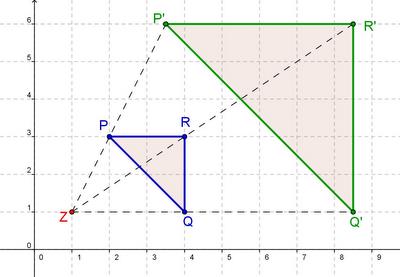
- c) Z(1|1), k= 2.5, P(2|3), Q(4|1), R(4|3)
- Hier kannst du deine Lösung mit der von Dia vergleichen:
a)
b)
c)
6. Station: Wissenswertes
- Auf dem Bild siehst du einen Pantographen. Dieses Zeichengerät wurde früher, als es noch keine Computer
- gab, benutzt, um zentrische Streckungen durchzuführen. Heutzutage wird er auch von technischen Zeichnern
- und Architekten verwendet.
