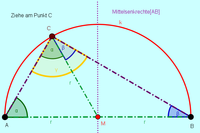
Erarbeitung von Grundwissen für den Satz des Thales

Lernpfad Erarbeitung von Grundwissen für den Satz des Thales

Ich bin der Thales-Clown

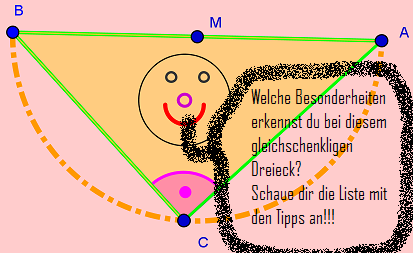
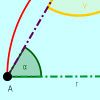
Weißt du eigentlich noch welche besonderen Eigenschaften so ein gleichschenkliges Dreieck hat?

Auf geht's - probiere einfach mal die erste Station aus!

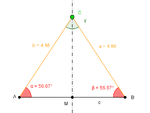
Erste Station:

Gleichschenkliges Dreieck:

Tipps und Lückentext:

Tipps: *Ziehe an dem grünen Punkt *Achte dabei auf die rot markierten Winkel *Was fällt dir bei den beiden orange markierten Schenkeln a und b auf? *Haben die beiden Winkel α und β irgendeine Besonderheit? Auf gehts - Ordne die richtigen Begriffe zu: Wenn ich am grünen Punkt ziehe, verändern sich die beiden Winkel und außerdem noch die beiden orange markierten Schenkel Schenkel a und Schenkel b. Auffallend ist zudem auch, dass der Winkel α immer das gleiche Winkelmaß besitzt, wie der Winkel β. Diese beiden Winkel α und β werden im auch Basiswinkel genannt. Die Strecke [AB] bezeichnet man in diesem gleichschenkligen Dreieck als Basisseite.

Die erste Station hast du also geschafft - naja, dann wird die zweite Station wohl erst recht klappen!

Viel Freude beim Multiple-Choice!

Zweite Station:

Gleichschenkliges Dreieck:

Auf gehts - Löse das Quiz:

Welche Seite wird Basis genannt? (Seite c) (!Seite a) (!Seite b) Welche Winkel sind Basiswinkel? (!γ) (α) (β) Die Strecke [MC] ist die Seitenhalbierende von: (!a) (!b) (c) Die Seiten a und b sind beide: (!so lang, wie Seite c) (gleich lang) (!niemals gleich lang) Die Winkel α + β + γ ergeben zusammen: (!360°) (!90°) (180°) Das Dreieck AMC ist kongruent zu: (!Dreieck ABC) (Dreieck MBC) Welche Seiten heißen im gleichschenkligen Dreieck Schenkel? (!c) (a) (b)

Ich bin der Thales-Clown

Dritte Station:

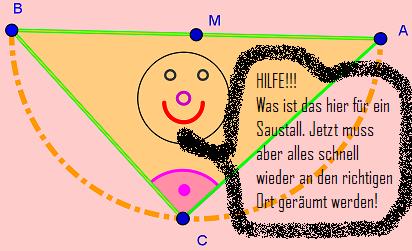
Jetzt wird aufgeräumt und Ordnung geschaffen!

Ordne die Bilder und Begriffe unten den richtigen Oberbegriffen zu!

Zuordnung

Die Strecken [AC] und [BC]	sind beide gleich lang	werden als Schenkel bezeichnet
Der Winkel im Punkt A ist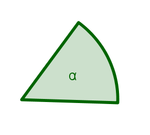
	hat das gleiche Winkelmaß wie β
Innenwinkelsumme im Dreieck =	180°	α + β + γ

Ich bin der Thales-Clown

So zum Abschluss noch ein letzter Test zu gleichschenkligen Dreiecken!

Danach bist du ein Spezialist auf diesem Gebiet!

Vierte Station:

Lies die folgenden Sätze konzentriert durch und klicke die korrekten Aussagen mit der linken Maustaste an.

1. Welche Aussage stimmt?

	In einem gleichschenkligen Dreieck sind mindestens zwei Seiten gleich lang.
	In einem gleichschenkligen Dreieck werden zwei gleich lange Seiten auch Basisseiten genannt.
	Die dritte Seite, die den beiden gleich langen Seiten gegenüberliegt, bezeichnet man als Schenkel.
	Die zwei gleich großen Winkel, die den Schenkeln gegenüberliegen, heißen Basiswinkel.

Gleichschenkliges Dreieck

2. Wie viele kongruente Dreiecke sind im Dreieck ΔABC enthalten?

	3
	2
	4

3. Welche Bezeichnungen hat die Strecke [MC]?

	Mittelsenkrechte zur Basis
	Winkelhalbierende des Winkels an der Spitze C
	Seitenhalbierende der beiden Schenkel
	Seitenhalbierende der Basis

4. Welche Gleichung ist richtig?

	180° - 2α = γ
	α = γ
	α = β
	α + β + γ = 180°

Punkte: 0 / 0

Ich bin der Thales-Clown

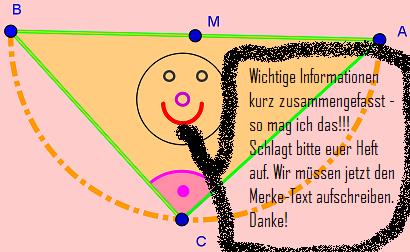
Jetzt fassen wir mal zusammen, was wir in den letzten vier Stationen gelernt haben.

Schlagt bitte euer Arbeitsheft auf und tragt den Merke-Text ein!

Merke Eigenschaften eines gleichschenkligen Dreiecks: Mindestens zwei Seiten sind gleich lang Basiswinkel sind gleich groß Die Innenwinkelsumme beträgt stets 180° Besitz von Achsensymmetrie

Ich bin der Thales-Clown

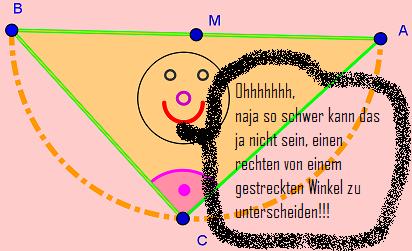
Kennst du noch den Unterschied zwischen einem stumpfen und einem spitzen Winkel?

Und weißt du noch was ein Nebenwinkel ist?

Ordne die Bilder und Begriffe unten den richtigen Oberbegriffen zu!

Fünfte Station:

Stufenwinkel Nebenwinkel Scheitelwinkel Nachbarwinkel Wechselwinkel

α = 180°: gestreckter Winkel α = 90°: rechter Winkel α < 90°: spitzer Winkel α > 90°: stumpfer Winkel

Ich bin der Thales-Clown

Also beim Memory war ich früher unschlagbar - wie schaut's mit dir aus?

Eine zusätzliche Wiederholung kann nicht schaden! Viel Spaß beim Memory!

Sechste Station:

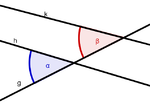
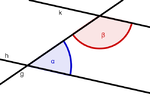
Stufenwinkel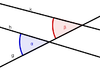
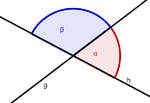
Nebenwinkel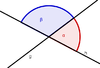
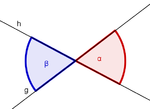
Scheitelwinkel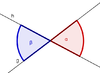
Nachbarwinkel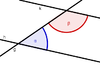
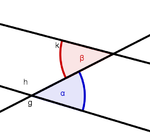
Wechselwinkel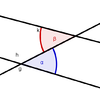
	α = 180°: gestreckter Winkel
	α = 90°: rechter Winkel
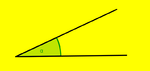
	α < 90°: spitzer Winkel
	α > 90°: stumpfer Winkel

Ich bin der Thales-Clown

So jetzt wird es aber wieder einmal Zeit zusammenzufassen, was wir gelernt haben.

Schlagt bitte euer Arbeitsheft auf und tragt den Merke-Text ein!

Merke Eigenschaften spezieller Winkel: Nebenwinkel: Wenn sich zwei Geraden schneiden, dann bezeichnet man ein Paar benachbarter Winkel als Nebenwinkel. Zudem ergänzen sich Nebenwinkel zu 180°. Scheitelwinkel oder Gegenwinkel: Wenn sich zwei Geraden schneiden, dann bezeichnet man das Paar gegenüberliegender Winkel als Scheitelwinkel oder Gegenwinkel. Außerdem sind Scheitelwinkel immer gleich groß. Stufen- oder F-Winkel: Wenn eine Gerade g zwei Geraden h und k schneidet, dann bezeichnet man den Winkel α und den Winkel β als Stufen- oder F-Winkel. Die Bedingung ist jedoch, dass - die beiden Winkel auf derselben Seite von g liegen. - beide entweder ober- oder unterhalb von h oder k liegen. Falls die beiden Graden h und k parallel sind, gilt: Stufenwinkel an Parallelen sind gleich groß. Wechselwinkel oder Z-Winkel: Wenn eine Gerade g zwei Geraden h und k schneidet, dann bezeichnet man den Winkel α und den Winkel β als Wechselwinkel oder Z-Winkel. Die Bedingung ist jedoch, dass - die beiden Winkel auf unterschiedlichen Seiten von g liegen und auf unterschiedlichen Seiten von h und k liegen. Falls die beiden Graden h und k parallel sind, gilt: :Stufenwinkel an Parallelen sind gleich groß. Nachbarwinkel oder E-Winkel: Wenn eine Gerade g zwei weitere parallele Geraden h und k schneidet, dann bezeichnet man den Winkel α und den Winkel β als Nachbar- oder E-Winkel. Die Bedingung ist jedoch, dass - die beiden Winkel auf derselben Seite von g liegen. - die beiden Winkel aber auf unterschiedlichen Seiten von h und k liegen. Zudem ergänzen sich Nachbarwinkel zu 180°.

Ich bin der Thales-Clown

Erinnerst du dich noch, wo und wann du zuletzt gepuzzlet hast?

Nun hast du den Auftrag dieses Puzzle zu machen!

Hast du eine Idee, was für ein Motiv das ist?

Viel Spaß beim Puzzle!!!

Siebte Station:

Ich bin der Thales-Clown

Eigentlich, müsstest du jetzt doch alles verstanden haben, oder?

Die nachstehenden Aufgaben kannst du in Absprache mit deinem Lehrer oder deiner Lehrerin bearbeiten!

Aufgabe   Arbeitsauftrag: Zeichne in dein Arbeitsheft ein gleichschenkliges Dreieck. Schreibe die besonderen Eigenschaften eines gleichschenkligen Dreiecks in dein Heft. Füge sonstige Besonderheiten hinzu, die dir während des Bearbeitens des Lernpfades aufgefallen sind.

Entstanden unter Mitwirkung von: Nico Stahl