3.Station

1. Station: Erster Vierstreckensatz - Schenkellösung - 2. Station: Erster Vierstreckensatz - Abschnittlösung - 3. Station: Zweiter Vierstreckensatz - 4. Station: Zusammenfassung - 5. Station: Übung

3. Station: Zweiter Vierstreckensatz

Auf dem Bild siehst du Panto neben einer 6 m hohen Kletterwand. Auch hier musst du wieder eine passende Formel zur

Berechnung der gesuchten Strecke x herleiten. Setze wieder die richtige Aussage in die passende Lücke ein:

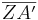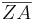
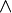
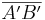$\overline{ZA'}$ = |k| ∙ $\overline{ZA}$ $\wedge$ $\overline{A'B'}$ = |k| ∙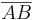 $\overline{AB}$
Aufgelöst nach |k|:
|k| = 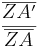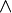${\overline{ZA'}\over\overline{ZA}}$ $\wedge$ |k| = ${\overline{A'B'}\over\overline{AB}}$
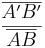
Gleichsetzen: ${\overline{ZA'}\over\overline{ZA}}$ = ${\overline{A'B'}\over\overline{AB}}$

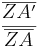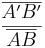
Fantastisch! Du hast hier den zweiten Vierstreckensatz hergeleitet. Er sagt aus, dass sich die Streckenabschnitte auf den

Parallelen, wie die zugehörigen Streckenlängen (von Z ausgehend) auf einer Geraden verhalten.

Berechne jetzt die Aufgabe in deinem Heft und trage hier deine Lösung mit Angabe der Einheit (cm) ein!

x= 0,30 cm (Tipp: Leerzeichen zwischen Zahl und Einheit nicht vergessen!).

Wenn du wissen willst, ob es Panto auf die Kletterwand geschafft hat, dann lass es dir anzeigen.

[Anzeigen][Verstecken]

Weiter zur 4. Station: Zusammenfassung

Zurück zur 2. Station: Erster Vierstreckensatz - Abschnittlösung