Calculators, Power Series and Chebyshev Polynomials
Originating author: Graeme Cohen
(THIS ARTICLE IS CURRENTLY BEING REVISED.)
Originating author: Graeme Cohen
Of all the familiar functions, such as trigonometric, exponential and logarithmic functions, surely the simplest to evaluate are
polynomial functions. The purposes of this article are, first, to introduce the concept of a power series, which can be thought
of as a polynomial function of infinite degree, and, second, to show their application to evaluating functions on a calculator.
When a calculator gives values of trigonometric or exponential or logarithmic functions, the most straightforward way is to
evaluate polynomial functions obtained by truncating power series that represent those functions and are sufficiently good
approximations. But there are often better ways. We will, in particular, deduce a power series for  and
will see how to improve on the straightforward approach to approximating its values. That will involve
Chebyshev polynomials, which are used in many ways for a similar purpose and
in many other applications, as well. (For trigonometric functions, the Cordic algorithm is
in fact often the preferred method of evaluation---the subject of another article here, perhaps.)
and
will see how to improve on the straightforward approach to approximating its values. That will involve
Chebyshev polynomials, which are used in many ways for a similar purpose and
in many other applications, as well. (For trigonometric functions, the Cordic algorithm is
in fact often the preferred method of evaluation---the subject of another article here, perhaps.)
In the spirit of Felix Klein, there will be some reliance on a graphical approach. Other than that, we need only some basic trigonometry and calculus.
Inhaltsverzeichnis |
Manipulations with geometric series
The geometric series  is the simplest power series. The sum of the series exists when
is the simplest power series. The sum of the series exists when
 . In fact,
. In fact,
The general form of a power series is
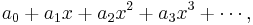
so the geometric series above is a power series in which all the coefficients 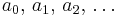 are equal to
1. In this case, since the series converges to
are equal to
1. In this case, since the series converges to 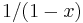 when
when 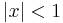 , we say that the function
, we say that the function
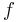 , where
, where

has the series expansion 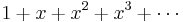 , or that
, or that 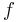 is represented by this series. We are
interested initially to show some other functions that can be represented by power series.
is represented by this series. We are
interested initially to show some other functions that can be represented by power series.
Many such functions may be obtained directly from the result in (1). For example, by replacing  by
by
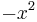 , we immediately have a series representation for the function
, we immediately have a series representation for the function  :
:
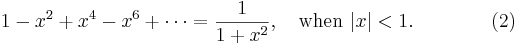
We can differentiate both sides of (1) to give a series representation of the function 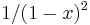 :
:
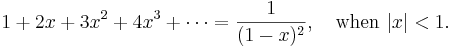
We can also integrate both sides of (1). Multiply through by 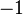 (for convenience), then write
(for convenience), then write 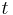 for
for
 and integrate with respect to
and integrate with respect to 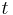 from 0 to
from 0 to  , where
, where 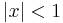 :
:
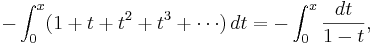
so

So this gives a series representation of the function 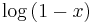 for
for 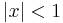 . In the same way, from
(2),
. In the same way, from
(2),
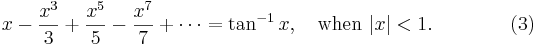
Much of what we have done here (and will do later) requires justification, but we can leave that to the textbooks.
The power series for the sine function
We will show next how to find a power series representation for 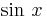 . In general terms, we can write
. In general terms, we can write
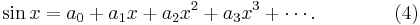
Put  , and immediately we have
, and immediately we have 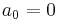 . Differentiate both sides of (4):
. Differentiate both sides of (4):
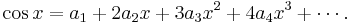
Again put  , giving
, giving 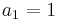 . Keep differentiating and putting
. Keep differentiating and putting  :
:
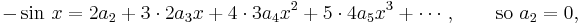
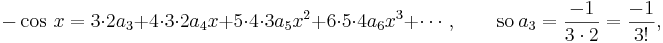
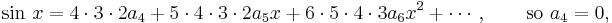

In this way, we can find a formula for all the coefficients  , namely,
, namely,
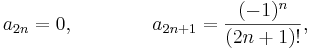
for 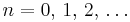 . (The coefficients of even index and those of odd index are specified separately.) Thus
. (The coefficients of even index and those of odd index are specified separately.) Thus
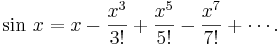
This is the power series representation that we were after. From the way we developed it, it is reasonable that the series will
represent  for values of
for values of  at and near 0 (say for
at and near 0 (say for 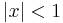 , as for all the
earlier examples), so it is surprising to know that it can be shown that the series represents
, as for all the
earlier examples), so it is surprising to know that it can be shown that the series represents 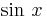 for all
values of
for all
values of  . Then partial sums of the series, obtained by stopping after some finite number of terms, should give
polynomial functions that can be used to find approximate values of the sine function, such as you find in tables of
trigonometric functions or as output on a calculator.
. Then partial sums of the series, obtained by stopping after some finite number of terms, should give
polynomial functions that can be used to find approximate values of the sine function, such as you find in tables of
trigonometric functions or as output on a calculator.
Approximation by Chebyshev Polynomials
For example, write

The cubic polynomial 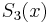 and the quintic polynomial
and the quintic polynomial 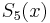 are plotted below, along with
are plotted below, along with
 , all for
, all for 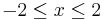 . It can be seen that these are both very good approximations for
. It can be seen that these are both very good approximations for
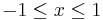 , say, but not so good near
, say, but not so good near 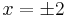 . The quintic
. The quintic  is much better than the
cubic
is much better than the
cubic  in these outer regions, as might be expected, but can we do better than
in these outer regions, as might be expected, but can we do better than  with some
other cubic polynomial function?
with some
other cubic polynomial function?
When 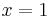 , for example, the error in using the cubic is
, for example, the error in using the cubic is 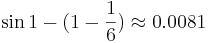 . We will
construct a cubic polynomial function
. We will
construct a cubic polynomial function  whose values differ from those of
whose values differ from those of  by less than
0.001 for
by less than
0.001 for 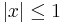 . The curve
. The curve 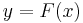 has been included in the graph below for
has been included in the graph below for 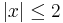 ,
and it is clear from the graph that this curve is closer to that of
,
and it is clear from the graph that this curve is closer to that of 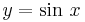 than
than 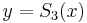 is, even
near
is, even
near 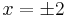 .
.
We will use Chebyshev polynomials to construct  . These are used extensively in approximation problems, as we
are doing here. They are the functions
. These are used extensively in approximation problems, as we
are doing here. They are the functions 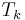 given by
given by
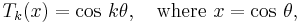
for integer  (or you can write
(or you can write 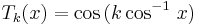 ). By properties of the cosine, they
all have domain
). By properties of the cosine, they
all have domain ![[-1,1]\,](/images/math/5/8/1/581a26dec23e9f937a02a278e20fc9c3.png) and their range is also in
and their range is also in ![[-1,1]\,](/images/math/5/8/1/581a26dec23e9f937a02a278e20fc9c3.png) . Putting
. Putting 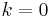 and
and
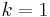 gives
gives

but it is not immediately apparent that the 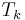 are indeed polynomials for
are indeed polynomials for  . To see that this is
the case, recall that
. To see that this is
the case, recall that
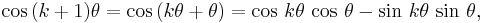
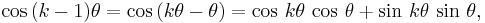
from which, after adding these,
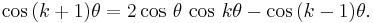
Therefore,

Now put  and obtain
and obtain


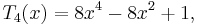
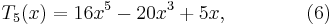
and so on, clearly obtaining a polynomial each time. As polynomials, we no longer need to think of their domains as restricted to
![[-1,1]\,](/images/math/5/8/1/581a26dec23e9f937a02a278e20fc9c3.png) .
.
Returning to our problem of approximating  for
for 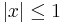 with error less than 0.001, we notice
first that the quintic
with error less than 0.001, we notice
first that the quintic  has that property. In fact,
has that property. In fact,

and the theory of alternating infinite series shows that 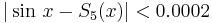 throughout our interval, as
certainly seems reasonable from the figure. We next express
throughout our interval, as
certainly seems reasonable from the figure. We next express 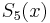 in terms of Chebyshev polynomials. Using (5)
and (6), we have
in terms of Chebyshev polynomials. Using (5)
and (6), we have
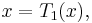

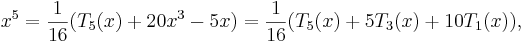
so
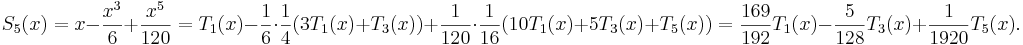
Since 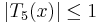 when
when 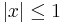 , omitting the term
, omitting the term 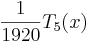 will admit a further
error of at most
will admit a further
error of at most 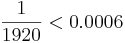 which, using (7), gives a total error less than 0.0008, still within our bound
of 0.001. Now,
which, using (7), gives a total error less than 0.0008, still within our bound
of 0.001. Now,
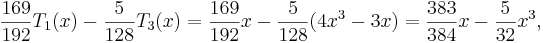
and the cubic function we end with is the function we called  .
.
We have thus shown, partly through a graphical justification, that values of the cubic function  , where
, where
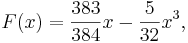
are closer to values of  , for
, for 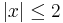 , than are values of the cubic function
, than are values of the cubic function
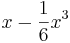 , which is obtained from the power series representation of
, which is obtained from the power series representation of 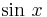 .
near
.
near 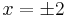 .
.
Conclusion --- The point of the story
The effectiveness of Chebyshev polynomials for such a purpose arises from properties of the cosine function. They tell us in
particular that for all integers  and for
and for 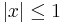 , we have
, we have 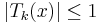 . Pafnuty
Lvovich Chebyshev was Russian; he introduced these polynomials in a paper in 1854. His surname is often given alternatively as
Tchebycheff, and this is why the polynomials are denoted with
. Pafnuty
Lvovich Chebyshev was Russian; he introduced these polynomials in a paper in 1854. His surname is often given alternatively as
Tchebycheff, and this is why the polynomials are denoted with 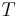 's.
's.
The procedure above is called economization of power series. As mentioned in the Introduction, there are other methods of
speeding up the calculation of values of the trigonometric functions, such as the Cordic algorithm for the sine function, but
economization is considered to be essential for slowly converging series such as that for 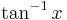 established in (3), above. Perhaps the point of this story is that, very often, the obvious approach is not necessarily best.
established in (3), above. Perhaps the point of this story is that, very often, the obvious approach is not necessarily best.