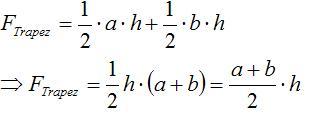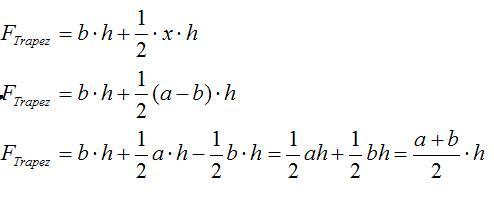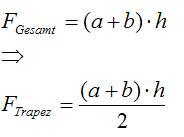Aufgabensammlung zur Flächeninhaltsberechnung

Es gibt ein Sprichwort, dass Du sicher kennst: "Übung macht den Meister!"

Werde zum Meister für Flächenberechnungen!

Genügend Übungen findest Du hier:

Aufgabe 1: Wie ändert sich der Flächeninhalt?

Du findest hier 10 Fragen. Fünf davon behandeln die Frage, wie sich der Flächeninhalt des Parallelogramms ändert, wenn eine oder

mehrere Maße im Parallelogramm verändert werden. Die anderen 5 Fragen sind auf das Dreieck bezogen!!

Hier geht es um das Parallelogramm:

Wie verändert sich der Flächeninhalt, im Parallelogramm, wenn...

Hier dreht sich alles um das Dreieck!

Wie ändert sich der Flächeninhalt im Dreieck, wenn...

Aufgabe 2: Nussecke backen

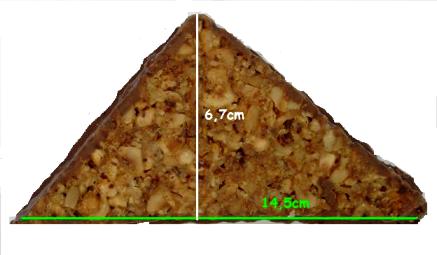
Maja hat 30 Nussecken gebacken und möchte deren Oberseite vollständig mit Schokolade überziehen. Das Bild zeigt eine Nussecke, die 6,7 cm hoch und 14,5 cm breit ist. Alle Nussecken sind gleich groß.

Frage: Für welche Fläche braucht Maja Schokolade?

Sie benötigt für eine Fläche von ( nur die Zahl eintragen!) cm² Schokolade

Aufgabe 3: Bayerische Fahne

Nils möchte fürs Oktoberfest eine bayerische Fahne nach seiner obigen Skizze nähen. Wieviel blauen und weißen Stoff in dm² braucht er?

Arbeitsauftrag

Berechne die Fläche auf 2 verschiedenen Wegen!

1. Weg: Tipp: Wieviele blaue und weiße Flächen sind auf der Fahne insgesamt?

Es gibt blaue Flächen wie Die Fahne ist (dm) hoch und (dm) breit.
Damit beträgt ihr Flächeninhalt (dm²)
Da die Hälfte der Fahne blau und die andere Hälfte weiß gefärbt ist, braucht Nils je ( in dm²) Stoff.

weiße Flächen.genauso viele

2. Weg: Tipp: Berechne zunächst den Flächeninhalt einer Raute, Zähle anschließend die Rauten und berechne den Flächeninhalt des blauen, bzw. weißen Stoffs!

Der Flächeninhalt einer Raute beträgt (dm²)
Es gibt insgesamt (ganze Rauten), (halbe Raute ) und (viertel Raute). Also insgesamt (gesucht wird die Dezimalzahl!)
Damit benötigt Nils jeweils (dm²) blauen und weißen Stoff.

Aufgabe 4: Variation Dreieck

Wie sieht die Flächeninhaltsformel für ein...

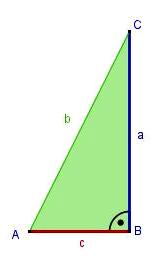
...rechtwinkliges Dreieck ABC aus?

Der rechte Winkel befindet sich am Eckpunkt C

Ergänze die fehlenden Felder und ermittle daraus die Flächeninhaltsformel für das rechtwinklige Dreieck:

Bei der Ergänzung gilt z.B.:
im Dreieck = Länge c
Seite im Dreieck = im Rechteck

Das rechtwinklige Dreieck ist so groß wie das entstehende Rechteck, daher gilt: F_rechtwinklig = $\cdot$ $\cdot$ a

im RechteckSeite cBreite ac ${1 \over 2}$ ahalb

Wie sieht die Flächeninhaltsformel für ein...

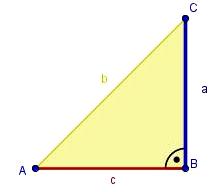
..gleichschenklig-rechtwinkliges Dreieck ABC aus?

Der rechte Winkel befindet sich am Eckpunkt C.

Ergänze die fehlenden Felder und ermittle daraus die Flächeninhaltsformel für das gleichschenklig-rechtwinklige Dreieck:

Bei der Ergänzung gilt z.B.:
im Dreieck = Seite c
Seite im Dreieck = im Quadrat
Im Quadrat gilt:

Das rechtwinklige Dreieck ist so groß wie das entstehende Quadrat, daher gilt:
F_{gleichschenklig-rechtwinklig} = $\cdot$ $\cdot$ a =

Seite aaa²a ${1 \over 2}$ im Quadrata = chalbSeite c

Aufgabe 5: Drachenviereck

In der folgenden Darstellung siehst Du ein Drachenviereck mit den Diagonalen e und f

Arbeitsauftrag:

Leite mit Hilfe der Flächeninhaltsformel des Dreiecks die Flächeninhaltsformel für das Drachenviereck her. Benutze dazu die Diagonalen e und f.

Das Drachenviereck besteht aus Dreiecke (orange - , sowie - gelb) Dieses Drachenviereck wurde zunächst . Die Teilfigur welche sich nun aus einem orangen und gelben Dreieck zusammensetzt, wurde zu einem ergänzt, indem man die des blauen und grünen Dreiecks jeweils an die Hypothenuse des gelben und orangen Dreiecks setzt. Aufgrund der gilt, dass Drachenviereck und Rechteck den besitzen. Die Diagonale e des Drachenvierecks enstpricht der und die Diagonale f der Länge des Rechtecks.
Damit ergibt sich für die Flächeninhaltsformel eines Drachenvierecks mit den Diagonalenlängen e und f:

F_{Drachenviereck} = e $\cdot$ =

Breite des RechteckshalbiertgrünZerlegungsgleichheitjeweils 2 Paaren kongruenter ${1 \over 2}$ e $\cdot$ fdoppeltenHypothenusegleichen Flächeninhalt ${1 \over 2}$ $\cdot$ fblauRechteck

Aufgabe 6: Trapez

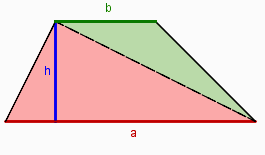
Hier siehst Du die Flächeninhaltsformel für das Trapez:

Es gibt verschiedene Varianten diese Formel herzuleiten. Auch Du kannst mit denen Dir zur Verfügung stehenden Mitteln, die Flächeninhaltsformel herleiten.

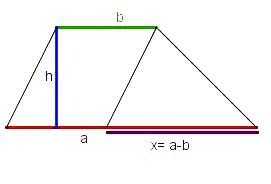
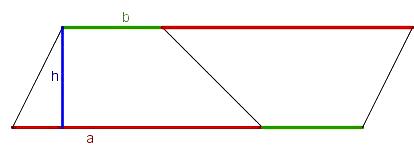
Du siehst hier 3 Bilder mit Lösungsideen zur Trapezberechnung. Dazu gibt es 3 entsprechende Rechenwegen, die die Lösungsidee repräsentieren:

Arbeitsauftrag:

1. Ordne den passenden Rechenweg dem richtigen Bild zu.

2.Übernehme eine Lösungsidee mit Bild und Rechenweg in Dein Heft

Ausgehend von bekannten Flächeninhaltsformeln lassen sich die Formeln für andere Figuren sehr leicht herleiten.
Dies erfordert allerdings viel Übung und auch einen Blick dafür, welche Teilfigur sich dahinter versteckt.

Welche Teilfiguren (Dreieck, Parallelogramm?) könnten sich denn hinter einem Sechseck verbergen??

Bearbeite dazu die nächste Aufgabe:

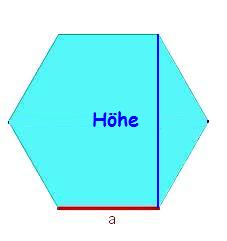
Aufgabe 7: Das Sechseck

Berechne den Flächeninhalt des gegebenen Sechsecks. Es besitzt die Seitenlänge a = 3 cm . Die Höhe ist 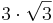$3\cdot \sqrt{3}$ cm hoch.

Runde auf die erste Nachkommastelle.

Das Sechseck hat einen Flächeninhalt von (cm²).

[Lösung anzeigen][Lösung ausblenden]

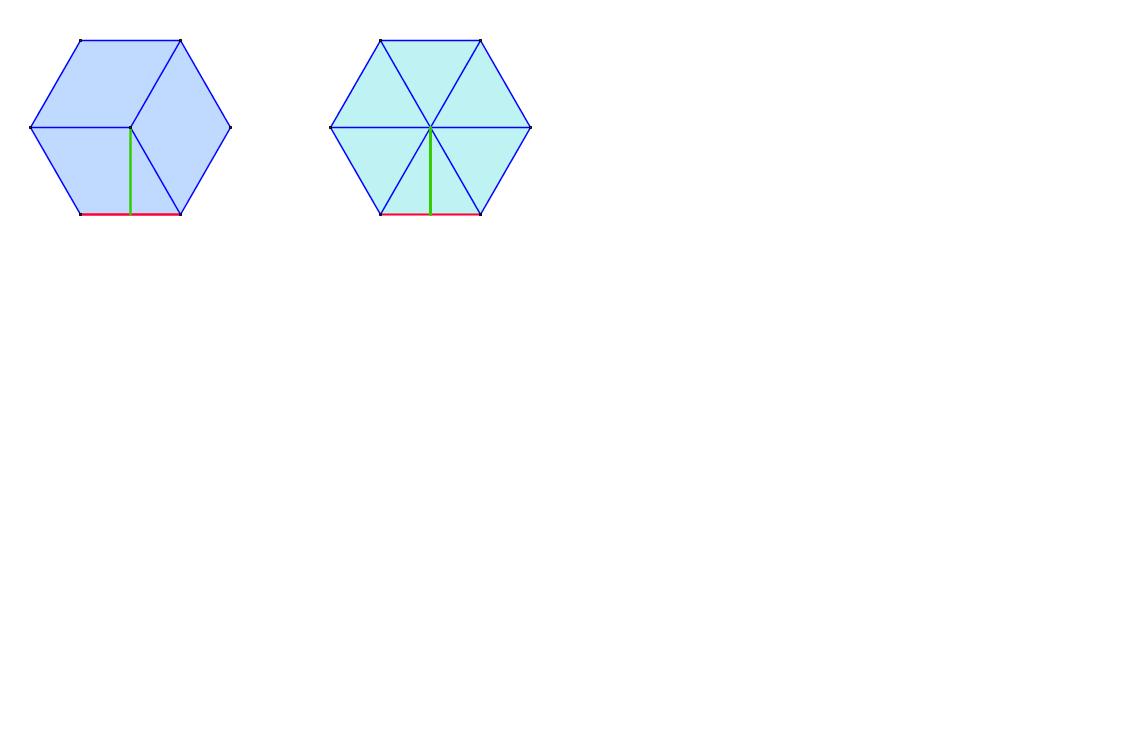
Für die Berechnung des Flächeninhalts eines regelmäßigen Sechsecks kannst Du natürlich mehrere Wege gehen. Hier siehst Du 2 Ansatzmöglichkeiten:

So ein regelmäßiges Sechseck setzt sich aus 6 gleichseitigen Dreiecken mit der Seitenlänge a bzw. aus 3 gleichseitigen Parallelogrammen mit der Seitenlänge a und jeweils der halben Höhe des Sechsecks zusammen:

Aufgabe 8: Umwandlungen

Gegeben ist ein Dreieck mit folgenden Maßen:

Länge der Höhe: 9cm
Länge der dazugehörigen Grundseite: 6cm

Arbeitsauftrag:

	Der Flächeninhalt wird halbiert
	Der Flächeninhalt wird vervierfacht
	Der Flächeninhalt gedrittelt
	Der Flächeninhalt wird bleibt gleich
	Der Flächeninhalt wird verdoppelt

	Der Flächeninhalt wird 6mal so groß
	Der Flächeninhalt wird gedrittelt
	Der Flächeninhalt wird ${1 \over 6 }$ mal so groß
	Der Flächeninhalt wird 3mal so groß

	Der Flächeninhalt wird 6 mal so groß
	Der Flächeninhalt wird verdoppelt
	Der Flächeninhalt wirt 4 mal so groß
	Der Flächeninhalt wird geviertelt

	Der Flächeninhalt wird 5 mal so groß
	Der Flächeninhalt wird 20 mal so groß
	Der Flächeninhalt wird 10 mal so groß
	Der Flächeninhalt wird 30 mal so groß
	Der Flächeninhalt wird 4 mal so groß

	Der Flächeninhalt wird verdoppelt
	Der Flächeninhalt wird vervierfacht
	Der Flächeninhalt wird halbiert
	Der Flächeninhalt wird verdreifacht

Aufgabensammlung zur Flächeninhaltsberechnung

Aufgabe 1: Wie ändert sich der Flächeninhalt?

Aufgabe 2: Nussecke backen

Aufgabe 3: Bayerische Fahne

Aufgabe 4: Variation Dreieck

Aufgabe 5: Drachenviereck

Aufgabe 6: Trapez

Aufgabe 7: Das Sechseck

Aufgabe 8: Umwandlungen

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge

	Der Flächeninhalt wird verdoppelt
	Der Flächeninhalt wird vervierfacht
	Der Flächeninhalt bleibt gleich
	Der Flächeninhalt wird halbiert
	Der Flächeninhalt wird geviertelt

	Der Flächeninhalt wird ${1\over 6}$ mal so groß
	Der Flächeninhalt wird 3 mal so groß
	Der Flächeninhalt wird ${1\over 3}$ mal so groß
	Der Flächeninhalt wird 6 mal so groß

	Der Flächeninhalt wird 2 mal so groß
	Der Flächeninhalt wird 4 mal so groß
	Der Flächeninhalt wird ${1\over 2}$ mal so groß
	Der Flächeninhalt wird ${1\over 4}$ mal so groß

	Man kann das Dreieck zu einem Parallelogramm mit der Seitenlänge c und der Höhe h ergänzen.
	Man kann das Dreieck zu einem Rechteck mit der Seitenlänge c und der Breite a ergänzen.
	Das Dreieck lässt sich zu einem Quadrat mit der Seitenlänge c ergänzen.

	Höhe: 3cm; Länge Grundseite: 9 cm
	Höhe: 9cm ; Länge Grundseite: 6 cm
	Höhe: 14cm; Länge Grundseite: 2 cm
	Höhe: $\sqrt{27}$ cm; Länge Grundseite: $\sqrt{27}$ cm
	Höhe: 9 cm; Länge Grundseite: 3cm
	Höhe: 4,5cm; Länge Grundseite: 6cm
	Höhe: 2 cm; Länge Grundseite: 13,5cm
	Höhe: 1 cm; Länge Grundseite: 27cm
	Höhe: 6,75 cm; Länge Grundseite: 4cm
	Höhe: 6 cm; Länge Grundseite:9cm