Wiederholung

Lernpfad In diesem Kapitel werden einige wichtige Grundlagen wiederholt

Bevor du dich mit dem Satz des Pythagoras beschäftigen kannst, musst du noch ein paar Grundlagen wiederholen.

Das ist ein Dreieck. Ich hoffe du kannst dich noch daran erinnern. Es hat drei Seiten und drei Eckpunkte. Blöderweise ist in der Zeichnung noch nichts beschriftet. Aber zum Glück bist du ein alter Dreieck-Profi und kannst das für mich übernehmen.

Aufgabe   Beschrifte die nachfolgende Zeichnung. Klicke dazu die Punkte und die Seitenbezeichnungen an und ziehe sie an die richtigen Stellen im Dreieck. Wenn du fertig bist, dann klicke auf das Kästchen!

Hast du es geschafft? Super, jetzt kenne ich mich wieder etwas besser aus.
Hier kannst du dir die Regeln noch einmal ansehen. [Anzeigen][Verstecken]

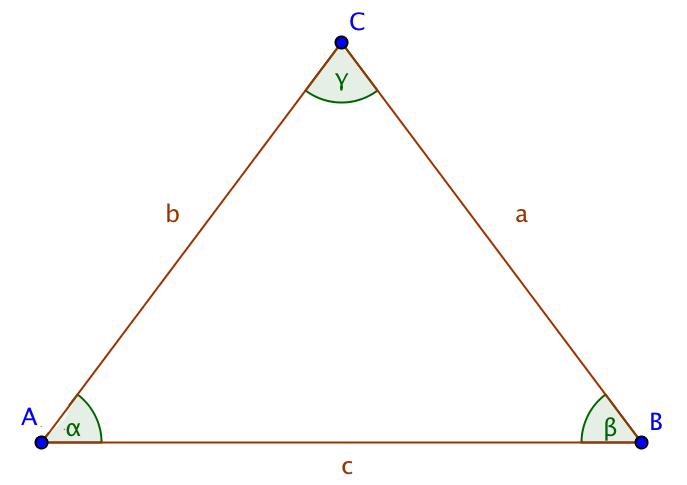
Merke Die Ecke, die der Seite a gegenüberliegt heißt A, die Ecke, die der Seite b gegenüberliegt heißt B, die Ecke, die der Seite c gegenüberliegt heißt C.

Diese Darstellung ist schon gut. Es fehlt aber noch etwas. Ein Dreieck hat doch auch noch drei Winkel? Ein komisches Wort, oder? Aber ihre Bezeichnungen sind noch komischer: α, β und γ. 1. Weißt du aus welcher Sprache die Bezeichnungen stammen? Deutsch Griechisch Spanisch Punkte: 0 / 0

Diese Darstellung ist schon gut. Es fehlt aber noch etwas.
Ein Dreieck hat doch auch noch drei Winkel?
Ein komisches Wort, oder? Aber ihre Bezeichnungen sind noch komischer: α, β und γ.

1. Weißt du aus welcher Sprache die Bezeichnungen stammen?

	Deutsch
	Griechisch
	Spanisch

Punkte: 0 / 0

Ich weiß leider nicht mehr genau wie sie angeordnet sind.
Aber zum Glück kannst du mir dabei ja helfen.

Aufgabe   Ordne die Winkel den richtigen Seiten zu und klicke danach auf Prüfen. Der Winkel an der Ecke A heißt α und wird gebildet von den Seiten b und c. Der Winkel an der Ecke B heißt β und wird gebildet von den Seiten a und c. Der Winkel an der Ecke C heißt γ und wird gebildet von den Seiten a und b.

Wunderbar!
Jetzt haben wir ja schon einiges zum Thema Dreieck wiederholt.
Ich habe dir noch einmal alles übersichtlich zusammengefasst: [Anzeigen][Verstecken]

Merke

Schauen wir doch einmal was du sonst noch so über Dreiecke weißt.

Aufgabe   Versuche herauszufinden, welches Dreieck zu welcher Beschreibung passt. Ordne die Beschreibungen den Dreiecken zu.

gleichschenkliges Dreieck	zwei Seiten sind gleich lang
spitzwinkliges Dreieck	alle drei Winkel < 90°
stumpfwinkliges Dreieck	ein Winkel > 90°
gleichseitiges Dreieck	alle drei Seiten sind gleich lang	alle drei Winkel sind gleich groß (60°)
rechtwinkliges Dreieck	ein Winkel beträgt genau 90°

Du warst dir ein wenig unsicher? Kein Problem - Ich habe dir die ganzen Regeln noch einmal übersichtlich zusammengefasst. [Anzeigen][Verstecken]

Merke gleichschenkliges Dreieck: zwei Seiten(zwei Schenkel) sind gleich lang spitzwinkliges Dreieck: alle drei Winkel <(kleiner als) 90° stumpfwinkliges Dreieck: ein Winkel >(größer als) 90° gleichseitiges Dreieck: alle drei Seitensind gleich lang; alle drei Winkel sind gleich groß (60°) rechtwinkliges Dreieck: ein Winkel beträgt genau 90°

Da du ja nun wieder ein echter Dreieck-Experte zu sein scheinst, können wir uns nun mit meinem Lieblingsdreieck beschäftigen, dem rechtwinkligen Dreieck.
Wollen wir doch mal sehen was dazu noch weißt.

Aufgabe   Verschiebe den Punkt C so, dass ein rechtwinkliges Dreieck entsteht. Klicke anschließend auf das Kästchen.

Super!
Um genau dieses Dreieck geht es im Satz des Pythagoras.
Die Seiten des rechtwinkligen Dreiecks haben besondere Bezeichnungen.

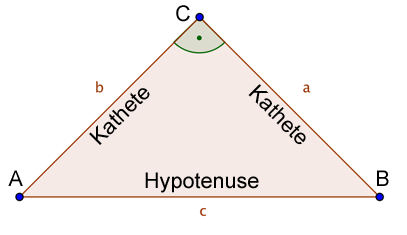
Merke In einem rechtwinkligen Dreieck heißt die längste Seite immer Hypotenuse und die anderen beiden Seiten Katheten. Die Hypotenuse liegt immer gegenüber des 90°-Winkels. Die beiden Katheten schließen immer den 90°-Winkel ein.

Du kannst dir das noch nicht richtig vorstellen? Kein Problem!
So sieht das grafisch aus:

Super! - Jetzt haben wir die wichtigen Sachen wiederholt.

Du bist nun soweit - Lass uns gleich loslegen!

Weiter zu Kapitel 2: Satz des Pythagoras