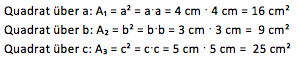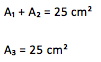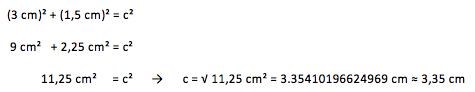Satz des Pythagoras
|
Lernpfad
|
Der Satz des Pythagoras funktioniert bei allen Dreiecken mit einem rechten Winkel.
Du bist ja nun schon ein richtiger Dreieck-Experte.
Wie war das noch gleich mit dem rechtwinkligen Dreieck?
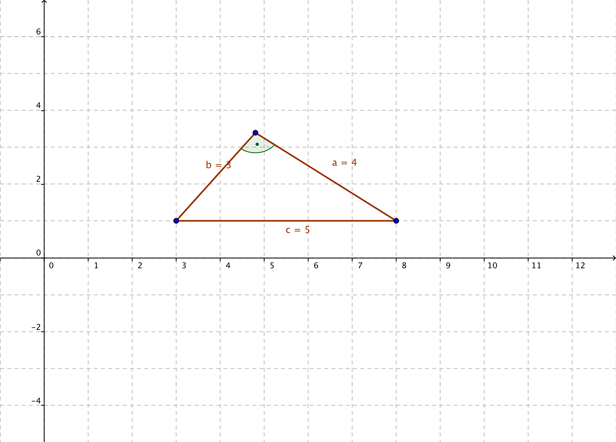
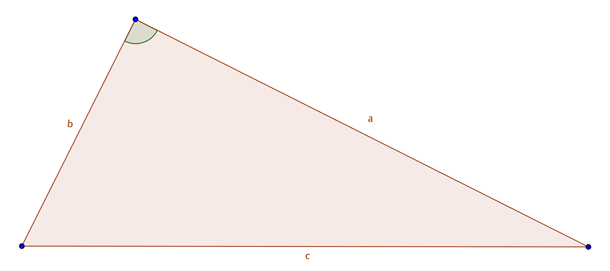
In dieser Zeichnung habe ich dir ein rechtwinkliges Dreieck mitgebracht.
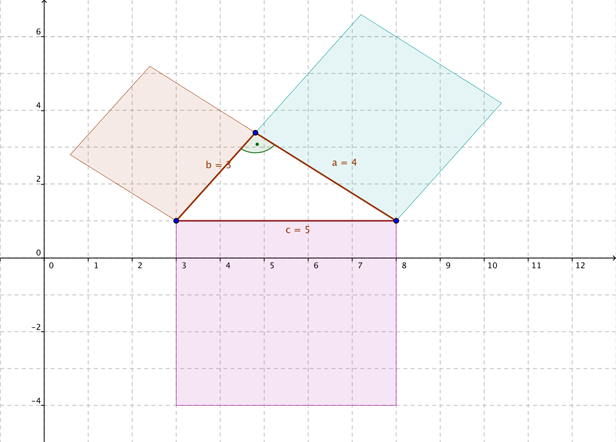
Ich habe über jeder Kathete und über der Hypotenuse jeweils ein Quadrat gemalt.
Die Seiten des Quadrats sind immer genauso lang wie die jeweilige Kathete oder Hypotenuse.
Wenn du auf „Abspielen“ drückst, kannst du dir anschauen, wie ich es gezeichnet habe.
Das war leicht, oder?
Die Fläche dieser Quadrate (A) kann man sogar ausrechnen.
Weißt du noch wie das geht? Schauen wir uns doch dazu ein Quadrat einmal genauer an:
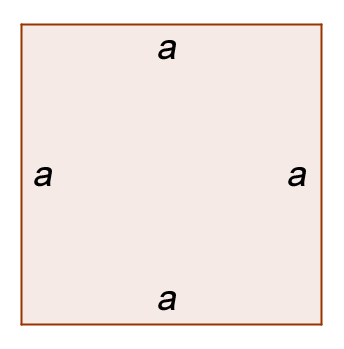
30px Merke
Die Fläche des Quadrats (A) berechnet man mit der Formel Länge mal Breite. |
So, jetzt bist du aber endlich soweit, dass du das Geheimnis erfahren darfst.
Pythagoras von Samos hat eine tolle Entdeckung gemacht.
Wenn du dir das nächste rechtwinklige Dreieck ansiehst, kommst du bestimmt selbst darauf.
Ich finde das super! Was hast du denn herausgefunden?
Halt! Verrate es noch nicht.
Versuche es mir doch mit Hilfe der nächsten Aufgabe zu erklären.
Genau! Wenn ich ein rechtwinkliges Dreieck habe und über den Seiten jeweils das Quadrat gemalt habe, dann sind die beiden Kathetenquadrate zusammen immer so groß wie das Hypotenusenquadrat.
Aber Vorsicht: Das gilt nur bei einem rechtwinkligen Dreieck.
Damit du das noch etwas besser verstehen kannst, möchte ich mit dir zusammen eine kleine Übungsaufgabe machen.
Schau sie dir mit mir zusammen einmal an.
Übungsaufgabe
1. Du hast ein rechtwinkliges Dreieck gegeben mit Hypotenuse c=5 cm, Kathete a=4 cm und Kathete b=3 cm.
2. Zeichne nun über jeder Seite ein Quadrat.
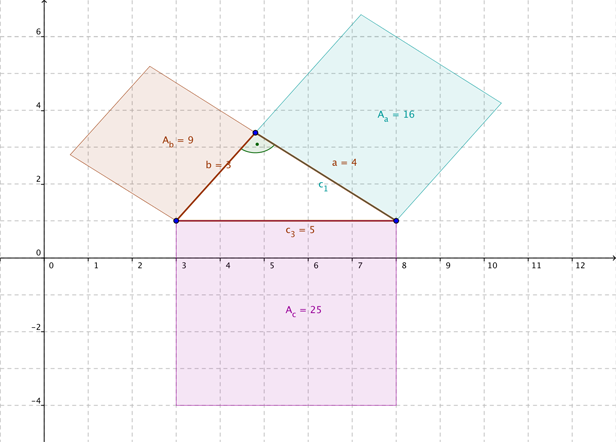
3. Berechne für jedes Quadrat den Flächeninhalt. Zur Erinnerung: A = a²
4. Addiere die Flächen der Quadrate über a und über b (=Kathetenquadrate).
5. Vergleiche dieses Ergebnis mit der Fläche des Quadrates über c (= A₃ = Hypotenusenquadrat).
6. Ergebnis:
Und? Bist du schon auf mein Geheimnis gekommen?
 |
Nun bist du schon ganz nahe dran. Ersetze nur noch die Flächen A₁, A₂ und A₃ durch ihre Formeln:
A₁ = a²
A₂ = b²
A₃ = c²
A₁ + A₂ = A₃ → a² + b² = c²
Super! Du hast das Geheimnis gelüftet.
Der Satz des Pythagoras
 |
a² + b² = c² |
Aber was kannst du damit anfangen?
Ich zeige es dir!
Du hast sicher Lust mit mir eine Pythagoras-Aufgabe zu rechnen.
Schau dir das mal an!
Rechenbeispiel
1. Formel aufstellen.
2. Gegebene Längenangaben in die Formel einsetzen.
3. Gleichung berechnen.
4. Lösung ermitteln.
War doch gar nicht so schwer, oder?
Jetzt kannst du dir bestimmt denken, was gegeben sein muss, wenn man den Satz des Satz des Pythagoras anwenden möchte?
Daraus können wir wieder einen Merksatz machen:
30px Merke
Sind in einem rechtwinkligen Dreieck die Längen von 2 Seiten bekannt, kann man die Länge der dritten Seite berechnen. |
Ich zeige dir, wie das geht.
Gegeben: Seite a = 4 cm und Seite c = 5 cm
Gesucht: Seite b?
a² + b² = c²
Ich möchte, dass „b²“ alleine auf einer Seite steht. Dazu bringe ich „a²“ auf die rechte Seite mit „–a²“. Ich rechne also auf beiden Seiten „-a²“!
a² + b² -a² = c² - a²
Auf der linken Seite fällt nun alles weg außer das „b²“, da „a²-a²“ ja „null“ ergibt. Alles andere kann ich nicht weiter ausrechnen und lasse es stehen.
b² = c² - a²
Und schon hast du die Formel so umgestellt, dass du die Seite b berechnen kannst, wenn du die Seiten a und c gegeben hast.
Genauso funktioniert das auch mit der Seite a.
Du erhälst dann die Formel: a² = c² - b²
Versuche doch mal das Puzzle richtig zu legen!
Puzzle: a² = c² - b² b² = c² - a² c² = a² + b²
30px Merke
{{{1}}} |
Schau dir die Formeln noch einmal genau an. Sie sind sehr wichtig und werden dir bei der Berechnung im Dreieck noch sehr nützlich sein.
Mehr kann ich dir zu meinem Geheimnis leider nicht mehr erzählen.
Aber ich denke, du wirst mir bei der Lösung der folgenden Aufgabe noch helfen können, oder?
Gegeben ist ein Dreieck mit den Seitenlängen c = 5cm und a = 4 cm. Berechnen sie die Seitenlänge b.
Super! Ich glaube, du bist jetzt wirklich ein Pythagoras-Experte.