Flächeninhalt Parallelogramm
Einstieg
- Lass uns hier gemeinsam die Formel für den Flächeninhalt des Parallelogramms erarbeiten. Du wirst sehen, es ist gar nicht so schwer!
- Hier siehst Du eine Möglichkeit, wie man die Flächeninhaltsformel von Parallelogrammen herleiten kann
Verschiebe das Dreieck und beobachte was passiert! Bearbeite dazu die nebenstehenden Fragen:
|
|
2. Begründe, warum ein Rechteck ensteht
Tipp: Denke an die Innenwinkelsumme im Dreieck und Paralellogramm! Lasse Dir dazu die Winkel anzeigen.
- Bearbeite dazu den folgenden Lückentext:
|
| 3. Welche Breite besitzt das Rechteck?
- Berechne den Flächeninhalt des Rechtecks.
In der Darstellung entspricht ein Kästchen einem Zentimeter.
Der Flächeninhalt des Rechtecks beträgt 12 (cm²)
Welchen Flächeninhalt besitzt das Parallelogramm?
Das Parallelogramm besitzt einen Flächeninhalt von 12 (cm²)
|
 |
- Wir haben das Parallelogramm in ein Trapez und ein rechtwinkliges Dreieck zerlegt.
- Anschließend wurd das Trapez durch Verschiebung des Dreiecks zum Rechteck ergänzt. Diese Verschiebung stellt eine Kongruenzabbildung dar.
- Das erhaltene Rechteck und das Ausgangsdreieck sind damit zerlegungsgleich und besitzen somit den gleichen Flächeninhalt.
Da diese Zerlegung und Ergänzung für alle Parallelogramme umsetzbar ist, können wir die Flächeninhaltsformel für Parallelogramme auf die Formel für Rechtecke zurückführen.
|
Hier geht es weiter zum nächsten Abschnitt:
Höhen im Parallelogramm

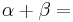 180°
180°
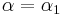
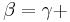 90° bzw.
90° bzw.
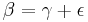
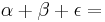 180°
180°

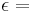 90° und
90° und 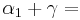 90°
90°


