Algebra: lineare Funktionen
Aus DMUW-Wiki
|
Jede Aussage ist entweder richtig oder falsch. Entscheide dich! |
Mit Hilfe der Schieberegler kannst du die Steigung und den y-Achsenabschnitt variieren!
|
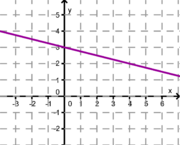
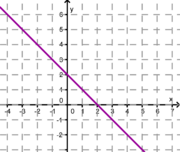
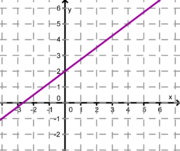
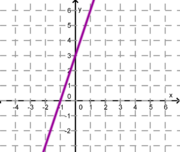
Ordne den Funktionsgraphen den richtigen Term zu.
2. Achte auf die Steigung und den y-Achsenabschnitt! Eine Geradengleichung bleibt übrig, diese ziehst du zum leeren Kästchen ganz rechts!
 Weiter zu 9. Klasse Algebra
Weiter zu 9. Klasse Algebra Zurück zu 8. Klasse Algebra
Zurück zu 8. Klasse Algebra
