Geraden am Kreis
|
Lernpfad
|
1. Aufgabe:
Mit dieser Aufgabe sollst du mit den verschiedenen Geraden am Kreis vertraut gemacht werden.
Ordne die Begriffe und Abbildungen richtig zu. Ziehe dafür die möglichen Lösungen mit gehaltener linker Maustaste in die Felder. Anschließend kannst du dein Ergebnis überprüfen. Hast du etwas falsch zugeordnet, kannst du anschließend diese Felder neu besetzen.
| Passante | Tangente | Sekante | Zentrale |
2. Aufgabe:
Benutze im linken Bild mit gehaltener linker Maustaste den Schieberegler und bearbeite danach die Aufgabe rechts daneben:
| Abstand: Gerade Kreis | Aufgabe |
|---|---|
|
Benutze den Schieberegler und löse damit das Quiz! Quiz: - Wieviele Zentralen enthält der Kreis? (!keine) (eine) (!zwei) (!ganz viele) - Welche Aussage ist bei Sekanten richtig? (!Die Strecke - Gibt es eine Passante, die einen Schnittpunkt mit dem Kreis k gemeinsam hat? (!ja) (nein) |
3. Aufgabe:
Mit dieser Aufgabe sollen nun die Eigenschaften der Geraden am Kreis festgehalten werden.
Ziehe dafür die möglichen Lösungen mit gehaltener linker Maustaste in die Felder. Anschließend kannst du dein Ergebnis überprüfen. Hast du etwas falsch zugeordnet, kannst du anschließend diese Felder neu besetzen.
- Ist der Abstand d der Gerade g zum Kreismittelpunkt M größer als der Radius r des Kreises, so nennt man die Gerade "Passante" (Schreibweise: d(M/g) > r).
- Sind Abstand der Geraden g zum Kreismittelpunkt M und Radius r gleich groß, so nennt man die Gerade "Tangente" (Schreibweise: d(M/g) = r).
- Ist der Abstand der Gerade g zum Kreismittelpunkt M kleiner als der Radius r des Kreises, so nennt man die Gerade "Sekante" (Schreibweise: d(M/g) < r). Spezialfall: Geht die Sekante durch den Mittelpunkt M des Kreises, so nennt man sie "Zentrale".
Tangentenkonstruktion mit dem Geodreieck
| Schritt 1 | ||
|---|---|---|
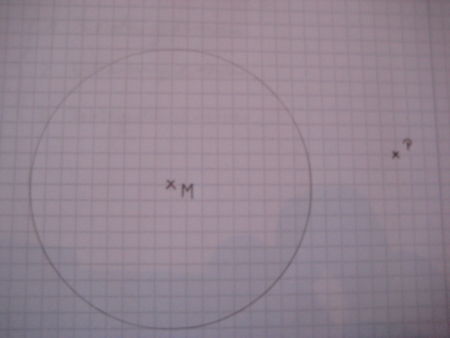 |
Hier siehst du einen Kreis und einen Punkt P außerhalb des Kreises. |
| Schritt 2 | ||
|---|---|---|
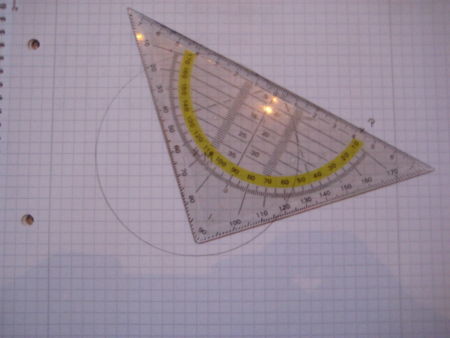 |
Jetzt musst du das Geodreieck so anlegen, dass dessen Zeichenkante den Punkt P und den Rand des Kreises berührt. |
| Schritt 3 | ||
|---|---|---|
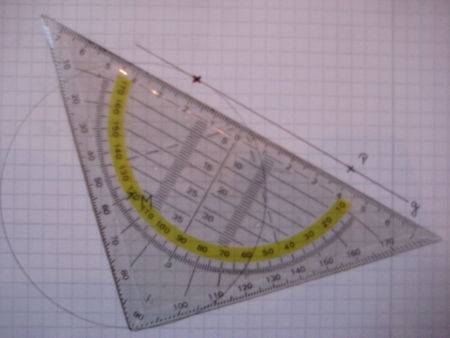 |
Als nächstes ziehst du eine Linie durch den Punkt P, die den Rand des Kreises in nur einem Punkt berührt. |
| Schritt 4 | ||
|---|---|---|
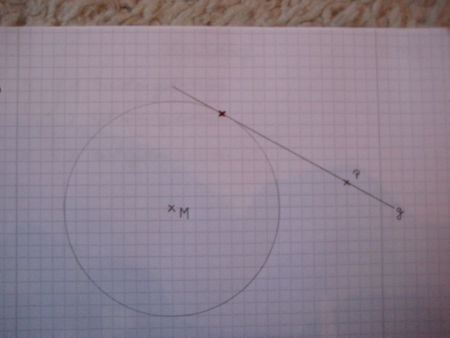 |
Jetzt hast du eine Tangente mit Hilfe des Geodreiecks konstruiert. |
Tangentenkontruktion mit dem Zirkel
| Schritt 1 | ||
|---|---|---|
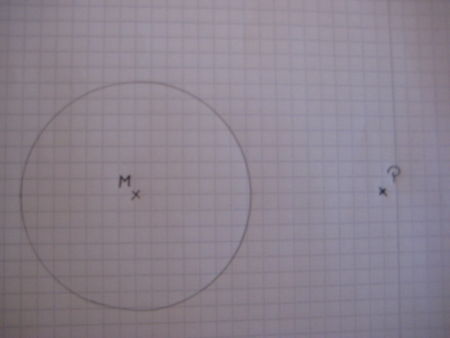 |
Hier siehst du einen Kreis und einen Punkt P außerhalb des Kreises. |
| Schritt 2 | ||
|---|---|---|
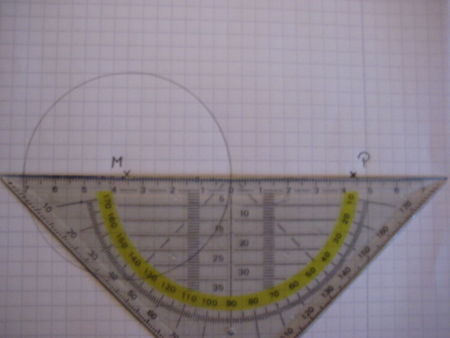 |
Jetzt musst du das Geodreieck so anlegen, dass dessen Zeichenkante den Punkt P und den Kreismittelpunkt M berührt. |
| Schritt 4 | ||
|---|---|---|
 |
Jetzt stichst du mit dem Zirkel in den Punkt Q, stellst als Radius die Entfernung zum Punkt P ein und zeichnest einen Kreis. |
| Schritt 5 | ||
|---|---|---|
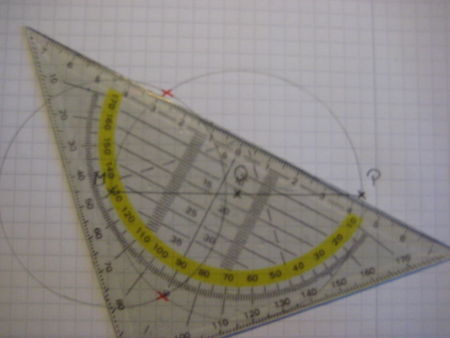 |
Dein neu gezeichneter Kreis hat zwei Schnittpunkte mit dem vorher gegebenen Kreis. Verbinde nun den Punkt P mit einem der zwei Schnittpunkte. |
| Schritt 6 | ||
|---|---|---|
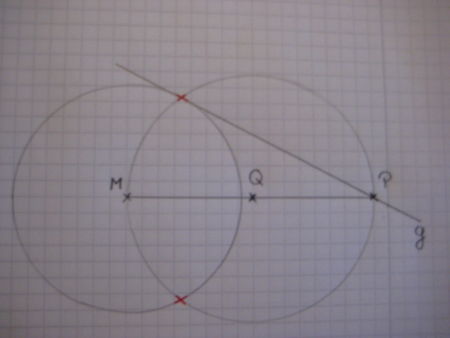 |
Jetzt hast du eine Tangente mit Hilfe des Zirkels konstruiert. |
1. Aufgabe:
Es gehören immer drei Kärtchen zueinander. Finde sie alle!

Spezialfall:
ZentraleSpezialfall:
2 Schnittpunkte;
Gerade durch den Kreismittelpunkt
Tangente 1 Schnittpunkt 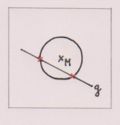
Sekante 2 Schnittpunkte 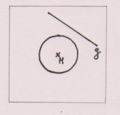
Passante kein Schnittpunkt
2. Aufgabe:
Im Alltag kommen auch Tangenten, Sekanten und Zentralen vor.
Lass uns neue Namen erfinden!
Schreibe folgendes Merke (ohne die Zeichnungen) in dein Heft!30px MerkeEine Gerade kann mit einem Kreis
- keinen Schnittpunkt gemeinsam haben. Dann nennt man sie Passante.
- einen Schnittpunkt gemeinsam haben. Dann nennt man sie Tangente.
(Vergleiche:
 Tangenten-Panzerkette)
Tangenten-Panzerkette)
- zwei Schnittpunkte gemeinsam haben. Dann nennt man sie Sekante.
(Vergleiche:
 Sekanten-Gitarre)
Sekanten-Gitarre)
- zwei Schnittpunkte gemeinsam haben und durch den Kreismittelpunkt gehen. Dann nennt man sie Zentrale.
(Vergleiche:
 Zentralen-Pendeluhr)
Zentralen-Pendeluhr)
3. Aufgabe:Finde die verschiedenen Geraden am Kreis! (Waagrecht, senkrecht und schräg; gefundene Wörter werden grün markiert. Halte dabei die linke Maustaste gedrückt, um das Wort zu markieren)
Passante Sekante Tangente Zentrale
Glückwunsch!!
Du hast den ersten Lernpfad erfolgreich abgeschlossen! Im nächsten Lernpfad lernst du kennen, wie sich Geraden zueinander verhalten können, aber siehe selbst!
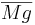 ist größer als der Radius r) (!Die Strecke
ist größer als der Radius r) (!Die Strecke 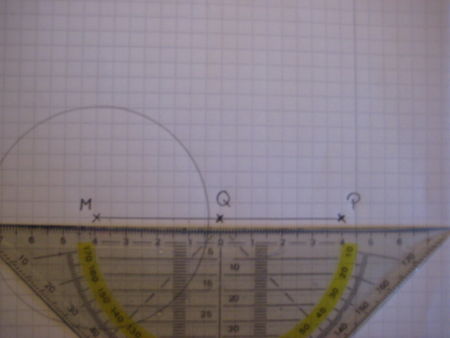


 Weiter zum Lernpfad Geraden zueinander
Weiter zum Lernpfad Geraden zueinander Zurück zur Hauptseite
Zurück zur Hauptseite
