Seite 2

Teilaufgabe b)

Wenn du am Schieberegler ziehst, kannst du das Flugzeug ein Looping fliegen lassen.

Um wieviel Grad wurde das Flugzeug gedreht, wenn es
a) das ganze Looping,
b) die Hälfte des Loopings,
c) $\frac{1}{4}$ des Loopings,
d) $\frac{3}{4}$ des Loopings
geflogen ist?

a) 360(°),
b) 180(°),
c) 90(°),
d) 270(°)

Schauen wir uns die Drehung um 90° noch einmal ein bisschen genauer an!

Welche Koordinaten hat der Bildpunkt zu A(12|14) nach einer um den Punkt Z(1|1) mit dem Drehwinkel α = 90°?
A' (-12 (x-Koordinate) | 12 (y-Koordinate))

Berechne die Verbindungvektoren 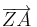$\overrightarrow { ZA }$ (Urvektor) und 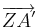$\overrightarrow { ZA' }$ (Bildvektor)!
Weißt du nicht mehr wie man Vektoren berechnet, dann lass dir folgenden Tipp anzeigen! [Anzeigen][Verstecken]

{{{1}}}

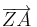$\overrightarrow { ZA }$ (11 (x-Koordinate) | 13 (y-Koordinate))
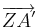$\overrightarrow { ZA' }$ > (-13 (x-Koordinate) | 11 (y-Koordinate))

1. Entscheide, welche der folgenden Aussagen zur Drehung um 90° richtig sind!

Verwende als Hilfe das Applet und die eben berechneten Vektoren.

	Die Strecken UrpunktZentrum und BildpunktZentrum stehen senkrecht aufeinander
	Man erhält die Koordinaten des Bildvektors ZP' durch vertauschen der Koordinaten des Urvektors ZP
	Die y-Koordinate des Bildvektors ZP' bekommt das umgekehrte Vorzeichen
	Die x-Koordinate des Bildvektors ZP' bekommt das umgekehrte Vorzeichen
	Beide Koordinaten der Bildvektors ZP' bekommen das umgekehrte Vorzeichen

Punkte: 0 / 0

Das war doch gar nicht so schwer, oder? Üben wir das noch einmal an zwei Beispielen!

1. Gib zuerst die Koordinaten des Verbindungsvektor ZC an, wenn der Punkt C(2|14) um den Punkt Z(1|1) um 90° gedreht wird!
ZC (1 (x-Koordinate) | 13 (y-Koordinate))

Nach dem was du gerade gelernt hast ist es jetzt ganz einfach, die Koordinaten des Vektors ZC' zu berechnen!
ZC' (-12 (x-Koordinate) | 1 (y-Koordinate))

2. Das Flugzeug wird jetzt um das Zentrum Z(4|-2) um 90° gedreht. Berechne den Verbindungsvektor ZC' (C(2|14)).
ZC (1 (x-Koordinate) | 6 (y-Koordinate))
ZC' (-6 (x-Koordinate) | 1 (y-Koordinate))

Welche Koordinaten hat der Punkt C'?
C' (-3 (x-Koordinate) | 9 (y-Koordinate))

→Du hast das toll gemacht! Auf geht's zur nächsten Teilaufgabe!