Lernpfad3 Seite 3

|
2. Addition von gleichnamigen Brüchen
Zum Frühstück hat Svenja schon  Liter Schokomilch getrunken. Nach Unterrichtsschluss hat sie auch ihre
Liter Schokomilch getrunken. Nach Unterrichtsschluss hat sie auch ihre  Liter Flasche Apfelsaftschorle leer getrunken.
Liter Flasche Apfelsaftschorle leer getrunken.
Wie viel Liter hat Svenja insgesamt getrunken?
Kreuze nun den richtigen Rechenweg an und klicke auf prüfen!, um zu sehen, ob du Recht hast.
(! +
+  =
= 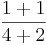 =
= 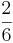 =
=  )
)
(! +
+  =
=  +
+  =
=  =
=  )
)
( +
+  =
=  +
+  =
= 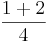 =
=  )
)
Hier siehst du, dass die beiden Brüche addiert werden, nachdem sie durch Erweitern auf denselben Hauptnenner gebracht werden (hier wurde mit 2 erweitert).
Für eine Schulfeier malen Svenja und ihre Mitschülerinnen und Mitschüler Bühnenbilder für das anstehende Schulfest.
Dazu mischen sie 2 verschiedene Farben:
 Liter rote Farbe und
Liter rote Farbe und  Liter gelbe Farbe
Liter gelbe Farbe
Wie viel Liter orange Farbe ergibt dies?
5 (Zähler) /4 (Nenner)
Kreuze die richtige Lösung an!
BEACHTE : Es können auch mehrere Lösungen richtig sein!
1) 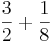 (!
(! ) (!
) (! ) (!
) (!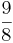 ) (!
) (!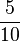 ) (
) (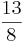 )
)
2) 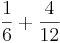 (!
(!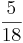 ) (
) (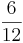 ) (!
) (!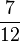 ) (
) ( ) (!
) (! )
)
3) 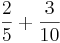 (!
(!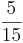 ) (
) (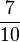 ) (!
) (! ) (!
) (!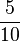 ) (!
) (! )
)
Damit du immer weisst, wie du bei der Addition ungleichnamiger Brüche vorgehen musst, fülle den Lückentext mit den richtigen Wörtern aus.
Das Beispiel soll dir eine kleine Hilfe sein.
| Allgemein: |
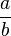 + + 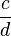 = = 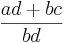
|
Beispiel Messbecher von oben:  Liter +
Liter +  Liter =
Liter =  Liter +
Liter +  Liter =
Liter =  Liter =
Liter = 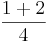 Liter =
Liter =  Liter
Liter


 +
+ 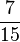
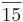
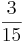 +
+ 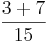 =
=