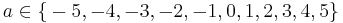Algebra: Potenzen und Potenzfunktionen: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
K
K
Zeile 3: Zeile 3:
 
| width=120px|
 
| width=120px|
  
−
[[Bild:Haas_parabel_gerader_ordnung.png|thumb|120px|Graph 1]]  
+
[[Bild:Haas_parabel_gerader_ordnung.png|thumb|200px|Graph 1]]  
  
−
[[Bild:Haas_parabel_ungerader_ordnung.png|thumb|120px|Graph 2]]  
+
[[Bild:Haas_parabel_ungerader_ordnung.png|thumb|200px|Graph 2]]  
  
 
|width="400"|
 
|width="400"|
Zeile 40: Zeile 40:
 
</quiz>
 
</quiz>
 
|width=120px|
 
|width=120px|
−
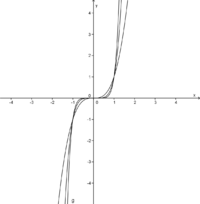
[[Bild:Haas_hyperbel_gerader_ordnung.png|thumb|120px|Graph 3]]  
+
[[Bild:Haas_hyperbel_gerader_ordnung.png|thumb|200px|Graph 3]]  
  
−
[[Bild:Haas_hyperbel_ungerader_ordnung.png|thumb|120px|Graph 4]]  
+
[[Bild:Haas_hyperbel_ungerader_ordnung.png|thumb|200px|Graph 4]]  
 
|}
 
|}
  

Version vom 8. Juli 2009, 09:59 Uhr

Graph 1
Graph 2

1. Klicke auf die jeweils zutreffenden Aussagen!

Graph 1 Graph 2 Graph 3 Graph 4
y = x^2
→ Alle Parabeln mit positiven, geraden Exponenten beschreiben diese Funktionen.
achsensymmetrisch
→ Parabeln und Hyperbeln gerader Ordnung sind symmetrisch zur x-Achse.
Parabel ungerader Ordnung
→ Diese Parabeleln haben positive, ungerade Exponenten.
\mathbb{D} = \mathbb{R}\setminus \{ 0\}  ; \mathbb{W} = \mathbb{R}\setminus \{ 0\}
→ Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!
Asymptoten x = 0; y = 0
→ Diese Graphen sind punktsymmetrisch und haben somit die beiden Achsen als Asymptoten.
\mathbb{D} = \mathbb{R}\setminus \{ 0\}  ; \mathbb{W} = \mathbb{R}^+
→ Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!
Hyperbel gerader Ordnung
→ Diese haben negative, gerade Exponenten.
y = x^{-7}
→ Alle Hyperbeln mit negativen, ungeraden Exponenten beschreiben diese Funktionen.
punktsymmetrisch
→ Parabeln und Hyperbeln ungerader ordnung sind punktsymmetrisch zum Ursprung
Scheitelpunkt im Ursprung
→ Die Koordinaten des Scheitelpunkts sind (0|0).
Symmetriepunkt im Ursprung
→ Die Koordinaten des Symmetriepunkts sind (0|0).
y = x^5
→ Alle Parabeln mit positiven, ungeraden Exponenten beschreiben diese Funktionen.
\mathbb{D} = \mathbb{R}
→ Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!

Punkte: 0 / 0
Graph 3
Graph 4

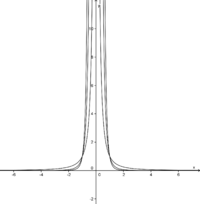
Hier kannst du mit dem Schieberegler den Parameter a der folgenden Gleichung variieren: 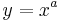y = x^a mit a \in \mathcal{f}-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5\mathcal{g}

Von „http://dmuw.zum.de/index.php?title=Aufgabentypen/Algebra:_Potenzen_und_Potenzfunktionen&oldid=2487“