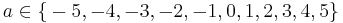Algebra: Potenzen und Potenzfunktionen: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
K
Zeile 14: Zeile 14:
 
| Graph 1 | Graph 2 | Graph 3 | Graph 4
 
| Graph 1 | Graph 2 | Graph 3 | Graph 4
 
+--- <math>y = x^2</math>
 
+--- <math>y = x^2</math>
−
|| Das ist eine Parabel mit einem positiven Exponenten.
+
|| Das ist eine Parabel mit einem geraden Exponenten.
 
+-+- achsensymmetrisch  
 
+-+- achsensymmetrisch  
 
|| Parabeln und Hyperbeln gerader Ordnung sind achsensymmetrisch zur y-Achse.
 
|| Parabeln und Hyperbeln gerader Ordnung sind achsensymmetrisch zur y-Achse.
Zeile 21: Zeile 21:
 
---+ <math>\mathbb{D} = \mathbb{R}\setminus \{ 0\} </math> ; <math>\mathbb{W} = \mathbb{R}\setminus \{ 0\} </math>  
 
---+ <math>\mathbb{D} = \mathbb{R}\setminus \{ 0\} </math> ; <math>\mathbb{W} = \mathbb{R}\setminus \{ 0\} </math>  
 
|| Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!
 
|| Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!
−
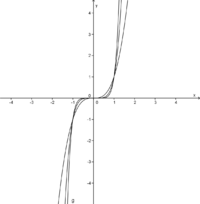
-+-+ Asymptoten x = 0; y = 0
+
--++ Asymptoten x = 0; y = 0
−
|| Diese Graphen sind punktsymmetrisch und haben somit die beiden Achsen als Asymptoten.
+
|| Alle Graphen mit negativen Exponenten nähern sich den Asymptoten an.
 
--+- <math>\mathbb{D} = \mathbb{R}\setminus \{ 0\} </math> ; <math>\mathbb{W} = \mathbb{R}^+</math>
 
--+- <math>\mathbb{D} = \mathbb{R}\setminus \{ 0\} </math> ; <math>\mathbb{W} = \mathbb{R}^+</math>
 
|| Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!
 
|| Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!
Zeile 28: Zeile 28:
 
|| Diese haben negative, gerade Exponenten.
 
|| Diese haben negative, gerade Exponenten.
 
---+ <math>y = x^{-7}</math>
 
---+ <math>y = x^{-7}</math>
−
|| Alle Hyperbeln mit negativen, ungeraden Exponenten beschreiben diese Funktionen.
+
|| Das ist eine Hyperbel mit ungeradem Exponenten.
 
-+-+ punktsymmetrisch
 
-+-+ punktsymmetrisch
 
|| Parabeln und Hyperbeln ungerader ordnung sind punktsymmetrisch zum Ursprung
 
|| Parabeln und Hyperbeln ungerader ordnung sind punktsymmetrisch zum Ursprung

Version vom 11. Juli 2009, 12:02 Uhr

Graph 1
Graph 2

1. Klicke auf die jeweils zutreffenden Aussagen!

Graph 1 Graph 2 Graph 3 Graph 4
y = x^2
→ Das ist eine Parabel mit einem geraden Exponenten.
achsensymmetrisch
→ Parabeln und Hyperbeln gerader Ordnung sind achsensymmetrisch zur y-Achse.
Parabel ungerader Ordnung
→ Diese Funktionen haben positive, ungerade Exponenten.
\mathbb{D} = \mathbb{R}\setminus \{ 0\}  ; \mathbb{W} = \mathbb{R}\setminus \{ 0\}
→ Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!
Asymptoten x = 0; y = 0
→ Alle Graphen mit negativen Exponenten nähern sich den Asymptoten an.
\mathbb{D} = \mathbb{R}\setminus \{ 0\}  ; \mathbb{W} = \mathbb{R}^+
→ Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!
Hyperbel gerader Ordnung
→ Diese haben negative, gerade Exponenten.
y = x^{-7}
→ Das ist eine Hyperbel mit ungeradem Exponenten.
punktsymmetrisch
→ Parabeln und Hyperbeln ungerader ordnung sind punktsymmetrisch zum Ursprung
Scheitelpunkt im Ursprung
→ Die Koordinaten des Scheitelpunkts sind (0|0).
Symmetriepunkt im Ursprung
→ Die Koordinaten des Symmetriepunkts sind (0|0).
y = x^5
→ Alle Parabeln mit positiven, ungeraden Exponenten beschreiben diese Funktionen.
\mathbb{D} = \mathbb{R}
→ Beim Werte- und Definitionsbereich musst du ganz genau aufpassen!

Punkte: 0 / 0
Graph 3
Graph 4

Hier kannst du mit dem Schieberegler den Parameter a der folgenden Gleichung variieren: 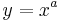y = x^a mit a \in \mathcal{f}-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5\mathcal{g}

Von „http://dmuw.zum.de/index.php?title=Aufgabentypen/Algebra:_Potenzen_und_Potenzfunktionen&oldid=2759“