Algebra: lineare Funktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
K |
||
| (28 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="border: 3px solid #551A8B ; background-color:#FFBBFF ; padding:7px;"><big><span style="color:#551A8B ">'''Lineare Funktionen</span>'''</big></div> | ||
| + | <br /> | ||
| + | <div style="border: 3px solid #551A8B ; background-color:#FFBBFF ; padding:7px;"> | ||
| + | '''Der Graph einer linearen Funktion ist eine Gerade der Form <span style="color: #551A8B ">y = mx + t.</span> Dabei bezeichnet <span style="color: #8B1C62">m</span> die <span style="color: #8B1C62">Steigung</span> der Geraden und <span style="color: #00C5CD ">t</span> den <span style="color: #00C5CD ">y-Achsenabschnitt</span>, das heißt den Schnittpunkt der Geraden mit der y-Achse.''' <br /> Damit du eine Gerade ins Koordinatensystem zeichnen kannst, brauchst du ja einige Angaben über Punkte etc. <br />'''Aber welche Angaben reichen zum Zeichnen einer Geraden und welche nicht?'''</div> | ||
| + | {| | ||
| + | |- | ||
| + | | width="450" | | ||
| + | <span style="color: #551A8B ">'''Jede Aussage ist entweder richtig oder falsch. Entscheide dich!'''</span> | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{ Eine Gerade g ist eindeutig bestimmt durch | { Eine Gerade g ist eindeutig bestimmt durch | ||
| typ="[]" } | | typ="[]" } | ||
| − | | | + | | richtig | falsch |
-+ ihre Steigung | -+ ihre Steigung | ||
| − | || Dazu brauchst du noch einen beliebigen Punkt! | + | || Dazu brauchst du noch einen beliebigen Punkt, von dem aus du das Steigungsdreieck zeichnen kannst! |
| − | +- einen beliebigen Punkt und den y-Achsenabschnitt | + | +- einen beliebigen Punkt und den y-Achsenabschnitt. |
| − | +- zwei beliebige Punkte | + | || Probiere es doch einmal aus ... es klappt! |
| − | +- ihren y-Achsenabschnitt und einem beliebigen Punkt auf der y-Achse | + | +- zwei beliebige Punkte. |
| − | || Die Gerade ist die y-Achse | + | || Durch die beiden Punkte wird die Steigung schon festgelegt. |
| − | -+ ihre Steigung und die Länge der Geraden | + | +- ihren y-Achsenabschnitt und einem beliebigen Punkt auf der y-Achse. |
| − | || Eine Gerade ist unendlich lang | + | || Die Gerade ist die y-Achse. |
| − | +- einen Punkt und eine zu g parallele Gerade | + | -+ ihre Steigung und die Länge der Geraden. |
| − | +- einen Punkt auf der x-Achse und ihre Steigung | + | || Achtung! Eine Gerade ist unendlich lang. |
| − | -+ ihre Steigung und eine zu g parallele Gerade | + | +- einen Punkt und eine zu g parallele Gerade. |
| − | || Du brauchst noch einen beliebigen Punkt | + | || Die parallele Gerade hat die gleiche Steigung wie g. |
| − | -+ ihr Steigungsdreieck | + | +- einen Punkt auf der x-Achse und ihre Steigung. |
| − | || | + | || Du hast einen Punkt, die Steigung... was willst du mehr? |
| − | -+ einen beliebigen Punkt und die Länge der Geraden | + | -+ ihre Steigung und eine zu g parallele Gerade. |
| − | || | + | || Du brauchst noch einen beliebigen Punkt, denn so hast du nur die Steigung. |
| − | +- drei beliebige Punkte | + | -+ einen beliebigen Punkt und ihr Steigungsdreieck. |
| + | || Das reicht natürlich zur eindeutigen Bestimmung! | ||
| + | -+ einen beliebigen Punkt und die Länge der Geraden. | ||
| + | || Wie gesagt...eine Gerade ist unendlich lang. | ||
| + | +- drei beliebige Punkte. | ||
| + | || Das klappt, es hätten auch zwei beliebige Punkte ausgereicht! | ||
</quiz> | </quiz> | ||
| + | || | ||
| + | ''Mit Hilfe der Schieberegler kannst du die Steigung und den y-Achsenabschnitt variieren!'' | ||
| + | <ggb_applet height="500" width="500" filename="Haas_Gerade.ggb" /> | ||
| + | |} | ||
| − | <div | + | <div style="padding:10px;background:#ffffff;border:1px ;"> |
| + | <span style="color: #551A8B ">'''Ordne den Funktionsgraphen den richtigen Term zu, indem du die passenden Geradengleichungen mit der linken Maustaste zu den Lücken unter den Graphen ziehst und den Begriff fallen lässt, wenn die Lücke rot wird.'''</span> | ||
| + | |||
| + | '''2.''' Achte auf die Steigung und den y-Achsenabschnitt! Eine Geradengleichung bleibt übrig, diese ziehst du zum leeren Kästchen ganz rechts. | ||
| + | |||
| + | <div class="lueckentext-quiz"> | ||
{| | {| | ||
| − | | [[Bild: | + | |- |
| − | + | | [[Bild:Haas_lingl1.png|180 px]] || [[Bild:Haas_lingl2.png|180 px]] || [[Bild:lingl3.png|180 px]]|| [[Bild:lingl4.png|180 px]] | |
| − | | [[Bild: | + | |- |
| − | + | | <strong> y = -0,25x + 3</strong> || <strong>y = -x + 2</strong> || <strong>y = 0,75x + 2</strong> || <strong>y = 3x + 3</strong> | |
| − | | [[Bild: | + | || <strong>y = 0,5x + 2</strong> |
| − | + | ||
| − | + | ||
|} | |} | ||
| − | </div> | + | |
| + | </div></div> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <div align="left">[[Aufgabentypen/Geometrie: Vierecke|<math>\Rightarrow</math> Weiter zu 9. Klasse Algebra]]</div> | ||
| + | <br> | ||
| + | <div align="left">[[Aufgabentypen/Geometrie: Geometrische Ortlinien und Ortsbereiche|<math>\Leftarrow</math> Zurück zu 8. Klasse Algebra]]</div> | ||
Aktuelle Version vom 31. Juli 2009, 10:37 Uhr
Lineare Funktionen
Der Graph einer linearen Funktion ist eine Gerade der Form y = mx + t. Dabei bezeichnet m die Steigung der Geraden und t den y-Achsenabschnitt, das heißt den Schnittpunkt der Geraden mit der y-Achse.
Damit du eine Gerade ins Koordinatensystem zeichnen kannst, brauchst du ja einige Angaben über Punkte etc.
Aber welche Angaben reichen zum Zeichnen einer Geraden und welche nicht?
Damit du eine Gerade ins Koordinatensystem zeichnen kannst, brauchst du ja einige Angaben über Punkte etc.
Aber welche Angaben reichen zum Zeichnen einer Geraden und welche nicht?
|
Jede Aussage ist entweder richtig oder falsch. Entscheide dich! |
Mit Hilfe der Schieberegler kannst du die Steigung und den y-Achsenabschnitt variieren!
|
Ordne den Funktionsgraphen den richtigen Term zu, indem du die passenden Geradengleichungen mit der linken Maustaste zu den Lücken unter den Graphen ziehst und den Begriff fallen lässt, wenn die Lücke rot wird.
2. Achte auf die Steigung und den y-Achsenabschnitt! Eine Geradengleichung bleibt übrig, diese ziehst du zum leeren Kästchen ganz rechts.
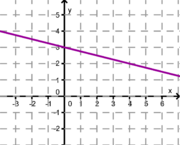
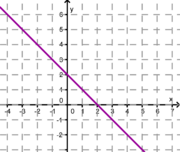
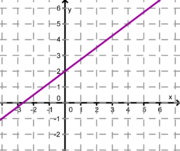
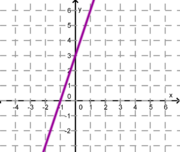
 Weiter zu 9. Klasse Algebra
Weiter zu 9. Klasse Algebra Zurück zu 8. Klasse Algebra
Zurück zu 8. Klasse Algebra
